C – Sasha and a Bit of Relax
其实这道题是一道大水题。我们知道成立条件为\(x_l \text{ xor } x_{l+1} \dots x_{mid} = x_{mid+1} \text{ xor } x_{mid+2} \dots x_{r}\)，然而这个运算可以直接移项：因为\(xor\)是自己本身的逆运算。然后为了保证\(r-l+1\)为偶数，我们只需要在 Trie 树末端维护奇偶计数即可。
Codeforces Round #551 (Div. 2) 解题报告 (CF1153)
C – Serval and Parenthesis Sequence
这道题主要是运用贪心。首先我们可以确定以下几种情况是肯定无解的：
- 第一个字符是 ‘)’，最后一个字符是 ‘(‘。
- 字符串长度为奇数。
我们发现整个字符串\(s[1 \dots n]\)中，第一个和最后一个字符一定要是 ‘(‘ 和 ‘)’。所以我们只用关心\(s[2 \dots n-1]\)就好。统计需要补充的括号个数：也就是\((n-2)\)减去现已确定的括号个数，分\(remL\)为左括号需要补充的个数、\(remR\)为右括号需要补充的个数。
P2154:「SDOI2009」虔诚的墓主人题解
解法
这道题很有意思啊。如果暴力枚举，答案式子：
\[ans = \sum_{x}^n \sum_{y}^m {up_{x,y} \choose k} {left_{x,y} \choose k} {right_{x,y} \choose k} {down_{x,y} \choose k}\]
其中\(up, left, right, down\)代表上下左右的常青树棵树。如何降低复杂度？
首先，我们可以考虑进行离散化：上下左右只要有为\(0\)的情况是不可能对答案有贡献的。然后，发现空隙中上下的部分：
CH3602:Counting Swaps 题解
主要思路
这是道好题，运用了图论建模的方法，可谓是十分精妙了。
对于每一个\(i\)与\(arr[i]\)都连一条有向边，比如说数列\(2\ 1\ 4\ 3\)：
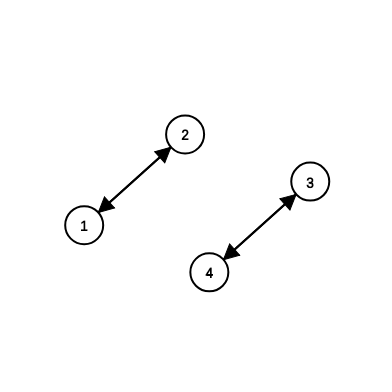
可以通过 DFS 染色的方式找出\(k\)个环，并且将每个环的长度记为\(l_i\)。我们可以得出一个引理：
在图中，对于长度为\(n\)的环，将其变为自环的最小步骤为\(n-1\)。
就是这样的性质，我们可以记\(F[i]\)为当环长为\(i\)时变为自环的方案数，那么我们可以基于分裂的思想，设\(T(x,y)\)为当环长为\(x+y\)时分裂为环长分别为\(x,y\)时的方案数，显然：
\[T(x,y) = \begin{cases} \frac{n}{2}, x = y \\ n, x \neq y \end{cases}\]
所以，我们可以照例推出：
\[ F[i] = \sum_{x+y=i} T(x,y)*F[x]*F[y]*\frac{(n-2)!}{(x-1)!(y-1)!} \]
我来解释一下这个式子的意义：首先，枚举\(x\)和\(y\)的情况，然后乘上这两个本身变成自环的方案数，也就是\(F[x]*F[y]\)，之后根据多重集排列公式和上面那个引理，两者步数分别为\(x-1,y-1\)，所以也不难得出上面那一坨了。
答案为\(\prod_{i = 1}^k {F_{l_i}} * \frac{(n-k)!}{\prod_{i = 1}^{k}(l_i-1)}\)，时间复杂度为\(O(n^2)\)，然而通过人类智慧等方法，发现\(F[n]=n^{n-2}\)，所以通过快速幂降为\(O(n \log n)\)。
代码
// CH3602.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 1e5 + 200, mod = 1e9 + 9;
int T, n, arr[MAX_N], head[MAX_N], current, k, li[MAX_N], vis[MAX_N];
ll level[MAX_N], inv[MAX_N];
struct edge
{
int to, nxt;
} edges[MAX_N << 1];
void addpath(int src, int dst)
{
edges[current].to = dst, edges[current].nxt = head[src];
head[src] = current++;
}
int dfs(int u, int fa)
{
vis[u] = true;
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].to != fa)
{
if (vis[edges[i].to])
return 1;
return dfs(edges[i].to, u) + 1;
}
return 1;
}
ll quick_power(ll bas, ll tim)
{
ll ans = 1;
while (tim)
{
if (tim & 1)
ans = ans * bas % mod;
bas = bas * bas % mod;
tim >>= 1;
}
return ans;
}
ll Fn(int n) { return (n == 1) ? 1 : quick_power(n, n - 2); }
int main()
{
scanf("%d", &T);
level[0] = inv[0] = 1;
for (int i = 1; i < MAX_N; i++)
level[i] = level[i - 1] * i % mod;
inv[MAX_N - 1] = quick_power(level[MAX_N - 1], mod - 2);
for (int i = MAX_N - 1; i >= 2; i--)
inv[i - 1] = inv[i] * i % mod;
while (T--)
{
memset(head, -1, sizeof(head)), current = 0;
memset(li, 0, sizeof(li)), k = 0;
memset(vis, 0, sizeof(vis));
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &arr[i]), addpath(arr[i], i), addpath(i, arr[i]);
for (int i = 1; i <= n; i++)
if (!vis[i])
li[++k] = dfs(i, 0);
ll ans = 1;
for (int i = 1; i <= k; i++)
ans = ans * Fn(li[i]) % mod;
ans = (ans * level[n - k] % mod);
for (int i = 1; i <= k; i++)
ans = ans * inv[li[i] - 1] % mod;
printf("%lld\n", ans);
continue;
}
return 0;
}
POJ1737:Connected Graph 题解
主要思路
这道题的计数方程和思想非常有趣，下面开始进行分析。
我们设\(F[i]\)为点数为\(i\)时的无向连通图种类。我们可以尝试容斥：\(n\)个点的无向图种类有\(2^{\frac{n(n-1)}{2}}\)，我们可以枚举\(k\)，删去大小为\(k\)的连通块来保持连通性。因为本题要求点标号，所以这些连通块的种类为：
\[\sum_{k=1}^{i-1}(F[k]*C_{i-1}^{j-1}*2^{\frac{(i-k)(i-k-1)}{2}})\]
其中，\(F[k]\)为连通块大小为\(k\)时的连通块个数，然后\(C_{i-1}^{j-1}\)是标号对答案的贡献，之后另一个残余块的种类为\(2^{\frac{(i-k)(i-k-1)}{2}}\)，乘起来即可。
这道题的加强版需要使用 NTT 和卷积的知识：BZOJ 3456:城市规划题解
代码
// POJ1737.cpp
//#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;
const int MAX_N = 60;
ll f[MAX_N], C[MAX_N][MAX_N], tmp;
int main()
{
C[1][0] = C[1][1] = 1;
for (int i = 2; i < MAX_N; i++)
{
C[i][0] = 1;
for (int j = 1; j < MAX_N; j++)
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
}
f[1] = 1;
for (int i = 2; i < MAX_N; i++)
{
f[i] = (1 << ((i * (i - 1)) >> 1));
for (int j = 1; j < i; j++)
f[i] -= f[j] * C[i - 1][j - 1] * (1 << (((i - j) * (i - j - 1)) >> 1));
}
while (~scanf("%d", &tmp) && tmp != 0)
printf("%lld\n", f[tmp]);
return 0;
}