我们可以把整个工作流程想像成网络流上的一条链：第\(i\)天连接到第\(i+1\)天的，流量为\(INF – A_i\)，费用为\(0\)；其中第\(n+1\)连接到汇点，流量为\(INF\)，费用为\(0\)；源点连接到点\(1\)，流量为\(INF\)，费用为\(0\)。
对于每一组志愿者\((s_i, t_i, c_i)\)，考虑连边\((s_i, t_i + 1, INF, c_i)\)，这样意味着整个工作流中可以从额外管道中获取流量，将最大流调整到\(INF\)。
所以求得的最小费用肯定是在最大流量\(INF\)的前提下求得的，即为答案。
大水题。
考虑按照给定数据建一张费用全部为 0 的图。跑完费用流求最大流输出答案之后，在现有的边的基础上加一条方向一致、容量无限、费用为\(w_i\)的边，最后开一个新点连接点\(n\)，容量为\(k\)即可。
这道题可以看作是网络流的一个模型了。我们把棋盘染色成红色和黑色。然后，源点连红色点，最大流限制为红点的点权；黑点全部连到汇点，最大流限制为黑点的点权。答案为点权总和减去最大流。
我们可以尝试理解一下：对于\(m = 1, n = 2\)的情况：
\[ [ x, y ] \]
那么假设\(x\)为黑点，\(y\)为红点，在网络上是这样的：
我们会发现最大流只会留下较小的一项。这样的话，我们可以感性推广到任何情况，大难点权和减掉最小割就行了。
这道题还是很有意思的，建图方式非常的巧妙。首先我们先把第一问的 DP 用 \(O(n \log n)\) 的时间求解一下，顺便搞到一个数组\(f[i]\)，含义是以\(i\)为结尾的最长子序列长度。建图的时候要注意的是，每一个位置对应的点要拆成两个：这是为了保持答案的唯一性。所以对于\(f[i]=1\)的点\(i\)，连边\((s,i)\)；对于\(f[i]=k\)的点\(i\)，连边\((i+n,t)\)。之后，如果对于\((u,v), f[v] = f[u] + 1, arr[u] \leq arr[v]\)进行连边，跑个最大流就可以出答案了。
第三问其实跟第二问的差不多，只需要把点\(1\)和点\(n\)的外向边（到源点或者是汇点的边）的最大流限制改成无穷大即可。
这道题其实跟 LOJ 6002 建模方式差不多，只是加了一个二分答案来进行动态建图。见代码：
// LOJ6003.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e4 + 100, INF = 0x3f3f3f3f;
int head[MAX_N], current, s, t, dep[MAX_N], cur[MAX_N], n, tot, upward[MAX_N], tag[MAX_N], unit;
struct edge
{
int to, nxt, weight;
} edges[500010];
void addpath(int src, int dst, int weight)
{
edges[current].to = dst, edges[current].weight = weight;
edges[current].nxt = head[src], head[src] = current++;
}
void add(int u, int v, int w) { addpath(u, v, w), addpath(v, u, 0); }
bool bfs()
{
queue<int> q;
q.push(s), memset(dep, 0, sizeof(dep));
dep[s] = 1;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].weight > 0 && dep[edges[i].to] == 0)
dep[edges[i].to] = dep[u] + 1, q.push(edges[i].to);
}
return dep[t] != 0;
}
int dfs(int u, int flow)
{
if (u == t || flow == 0)
return flow;
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (dep[edges[i].to] == dep[u] + 1 && (edges[i].weight > 0))
{
int to = edges[i].to, fl = dfs(to, min(flow, edges[i].weight));
if (fl > 0)
{
upward[u] = to;
if (u != s)
tag[edges[i].to - unit] = true;
edges[i].weight -= fl, edges[i ^ 1].weight += fl;
return fl;
}
}
return 0;
}
int dinic()
{
memset(tag, false, sizeof(tag));
int ans = 0;
while (bfs())
{
for (int i = 0; i <= tot; i++)
cur[i] = head[i];
while (int f = dfs(s, INF))
ans += f;
}
return ans;
}
bool check(int num)
{
unit = num;
tot = (num << 1) + 2, s = tot - 1, t = tot;
memset(head, -1, sizeof(head)), current = 0;
for (int i = 1; i <= num; i++)
add(s, i, 1), add(i + num, t, 1);
for (int i = 1; i <= num; i++)
for (int j = 1; j * j - i <= num; j++)
if (i < j * j - i)
add(j * j - i, i + num, 1);
return num - dinic() <= n;
}
int main()
{
scanf("%d", &n);
int l = 1, r = MAX_N - 2000, ans;
while (l <= r)
{
int mid = (l + r) >> 1;
if (check(mid))
l = mid + 1, ans = mid;
else
r = mid - 1;
}
printf("%d\n", ans);
check(ans);
for (int i = 1; i <= ans; i++)
if (!tag[i])
{
int p = i;
printf("%d ", p);
while (upward[p] && upward[p] != t && upward[p] - ans >= 0)
printf("%d ", upward[p] - ans), p = upward[p] - ans;
puts("");
}
return 0;
}
这个模型有点儿牛逼哦。
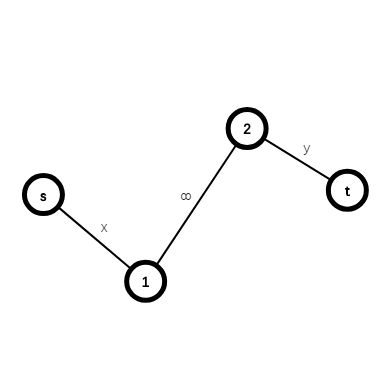
我们先来建一个网络。我们把我们得到的\(n\)个点复制一遍，变成第\(i\)与第\(i+n\)个点。让源点全部连接点域\([1,n]\)内的点，让点域\([n+1,2n]\)内的点全部连接汇点。如果有边\((u,v)\)，连接边\((u,v+n)\)。这里面所有的边容量都是\(1\)。求最大流做差即可。
我们把网络分层（把它想成 3D 的形状），第一层是源点和原生点，第二层是复制点和汇点。这两层之间的边都相当于有向无环图里的单向边，求最大流即可知道哪些不是路径覆盖中的点。
// LOJ6002.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 200 * 3, INF = 0x3f3f3f3f;
int n, m, head[MAX_N], current, upward[MAX_N], s, t, dep[MAX_N], cur[MAX_N], tmpx, tmpy;
bool tag[MAX_N];
struct edge
{
int to, nxt, weight;
} edges[6000 << 2];
void addpath(int src, int dst, int weight)
{
edges[current].to = dst, edges[current].weight = weight;
edges[current].nxt = head[src], head[src] = current++;
}
void add(int src, int dst, int w) { addpath(src, dst, w), addpath(dst, src, 0); }
bool bfs()
{
memset(dep, 0, sizeof(dep));
queue<int> q;
q.push(s), dep[s] = 1;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].weight > 0 && !dep[edges[i].to])
q.push(edges[i].to), dep[edges[i].to] = dep[u] + 1;
}
return dep[t] != 0;
}
int dfs(int u, int flow)
{
if (u == t || flow == 0)
return flow;
for (int &i = cur[u]; i != -1; i = edges[i].nxt)
if (edges[i].weight > 0 && dep[edges[i].to] == dep[u] + 1)
{
int to = edges[i].to, fl = dfs(to, min(edges[i].weight, flow));
if (fl > 0)
{
upward[u] = edges[i].to;
if (u != s)
tag[edges[i].to - n] = true;
edges[i].weight -= fl, edges[i ^ 1].weight += fl;
return fl;
}
}
return 0;
}
int Dinic()
{
int ans = 0;
while (bfs())
{
for (int i = 1; i <= 2 * n + 2; i++)
cur[i] = head[i];
while (int fl = dfs(s, INF))
ans += fl;
}
for (int i = 1; i <= n; i++)
if (!tag[i])
{
int p = i;
printf("%d ", p);
while (upward[p] && upward[p] != t)
printf("%d ", upward[p] - n), p = upward[p] - n;
printf("\n");
}
return ans;
}
int main()
{
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &m);
s = n * 2 + 1, t = s + 1;
for (int i = 1; i <= n; i++)
add(s, i, 1), add(i + n, t, 1);
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &tmpx, &tmpy);
add(tmpx, tmpy + n, 1);
}
printf("%d", n - Dinic());
return 0;
}