主要思路
我操这个题是真的有意思（做完后索然无味）。
肯定这个题状压 DP 没跑的，所以可以先设 \(f[S]\) 为集合 \(S\) 双连通的最小代价。直接做有点困难，我们需要思考一个归纳的方式来构造一个双连通图。
继续阅读“BZOJ3590:[SNOI2013]Quare – 题解”标签归档： 图论
AtCoder Grand Contest 038 – 解题报告
A – 01 Matrix
这个题还是很思博的，直接挂题解的图：
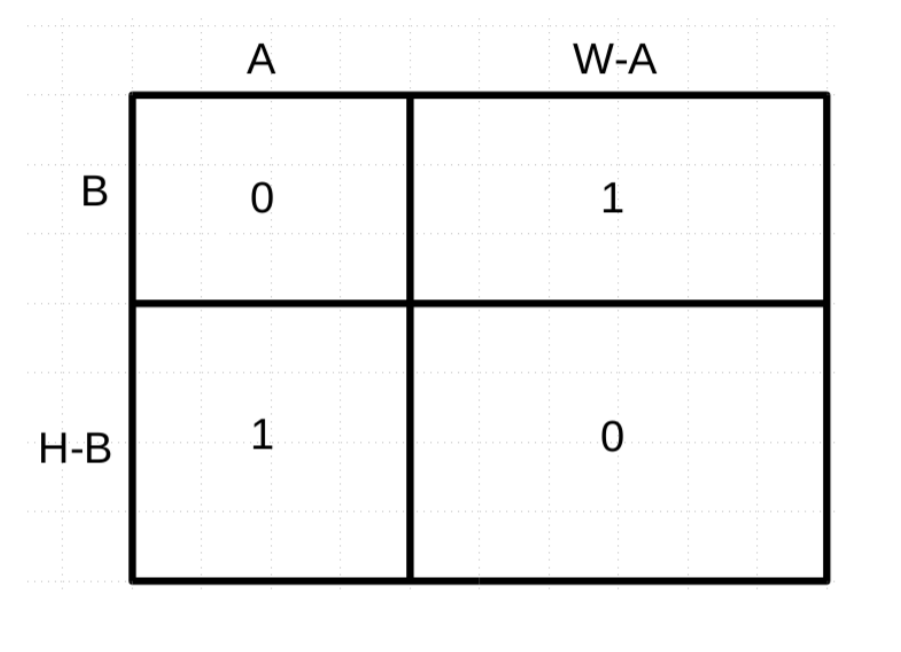
// A.cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, A, B;
scanf("%d%d%d%d", &n, &m, &B, &A);
for (int i = 1; i <= n; i++, puts(""))
for (int j = 1; j <= m; j++)
if ((i <= A) ^ (j <= B))
printf("1");
else
printf("0");
return 0;
}
继续阅读“AtCoder Grand Contest 038 – 解题报告” AtCoder Grand Contest 043 – 解题报告
A – Range Flip Find Route
思博题。考虑最后的路径肯定是多个黑白子路径的拼接，那么路径的代价就是进入黑色子路径的次数，那么我们只需要建图的时候给白色入黑色的边赋 \(1\) 的权即可。
继续阅读“AtCoder Grand Contest 043 – 解题报告”上下界网络流
「USACO 2018.12 Platinum」解题报告
A – The Cow Gathering
首先，如果没有限制的话，其实从叶子结点来抽是一定有解的，可以考虑思考一颗以最后出口为根结点的外向树来理解这个逻辑关系。现在有 \(m\) 个有向边，初步思考可以把每个点都作为最后一个节点，然后来看新的图有没有环，这样是 \(\Theta(n^2)\)。
AtCoder Regular Contest 099:E~F – 题解
E – Independence
这道题直接去想性质不好想，因为贪心的话、找到两个大小相近的团没什么性质。我们可以考虑建一张反图。如果这是个二分图，那么左右部恰好可以作为题中的两个 state。然而，意识到并不保证是一张连通的二分图，所以我们可以用一些连通块来拼成两个 state。那么，我们可以用个背包搞搞，再最后算算答案即可。（就不需要贪心的构造两个大小相近的团了，全部都算一遍即可）。