Miller-Rabin 素数测试
首先，强烈推荐阅读这篇文章。（看懂了就不用来了）
Miller-Robin 算法包括两个部分，一个是费马测试，还有一个就是二次探测。这两个东西听上去非常的玄学（的确也是），我来讲清楚，并附上代码。我们现在要进行测试的数是\(p\)。
Codeforces Round #551 (Div. 2) 解题报告 (CF1153)
C – Serval and Parenthesis Sequence
这道题主要是运用贪心。首先我们可以确定以下几种情况是肯定无解的：
- 第一个字符是 ‘)’，最后一个字符是 ‘(‘。
- 字符串长度为奇数。
我们发现整个字符串\(s[1 \dots n]\)中，第一个和最后一个字符一定要是 ‘(‘ 和 ‘)’。所以我们只用关心\(s[2 \dots n-1]\)就好。统计需要补充的括号个数：也就是\((n-2)\)减去现已确定的括号个数，分\(remL\)为左括号需要补充的个数、\(remR\)为右括号需要补充的个数。
LibreOJ 6007:「网络流 24 题」方格取数题解
解法
这道题可以看作是网络流的一个模型了。我们把棋盘染色成红色和黑色。然后，源点连红色点，最大流限制为红点的点权；黑点全部连到汇点，最大流限制为黑点的点权。答案为点权总和减去最大流。
我们可以尝试理解一下：对于\(m = 1, n = 2\)的情况：
\[ [ x, y ] \]
那么假设\(x\)为黑点，\(y\)为红点，在网络上是这样的：
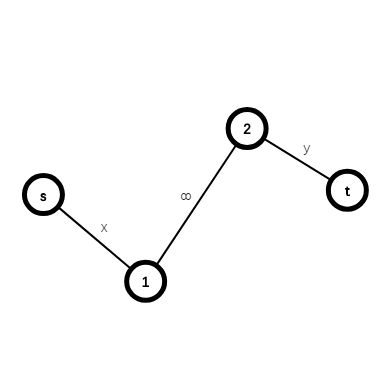
我们会发现最大流只会留下较小的一项。这样的话，我们可以感性推广到任何情况，大难点权和减掉最小割就行了。
「Codeforces 1138D」Camp Schedule 题解
解法
这道题其实就是考察 KMP 算法中 Next 数组的使用。题意转换过来大致就是：
给定两个 01 串，构造一个长度跟第一个串相同且 1 的个数相同的串，且保证第二个串的出现次数最多，出现可以重叠。
CH4701:天使玩偶题解
解法
这道题可以算是 CDQ 分治的一道基础题了。
首先，CDQ 分治的主要方式就是通过分治的方式将一段区间内操作和询问部分固定，变成静态子问题来解决（前提是每一个询问的答案都受过去的操作影响，且这些操作对问题的影响是独立的，也就是说回答询问为过去独立操作的叠加，答案不受顺序的影响）。
在本题中，我们先把初始点变成加点操作，这样就可以统一化了。每个询问的计算式：
P2154:「SDOI2009」虔诚的墓主人题解
解法
这道题很有意思啊。如果暴力枚举，答案式子：
\[ans = \sum_{x}^n \sum_{y}^m {up_{x,y} \choose k} {left_{x,y} \choose k} {right_{x,y} \choose k} {down_{x,y} \choose k}\]
其中\(up, left, right, down\)代表上下左右的常青树棵树。如何降低复杂度？
首先，我们可以考虑进行离散化：上下左右只要有为\(0\)的情况是不可能对答案有贡献的。然后，发现空隙中上下的部分：