主要思路
考虑设 \(S = \oplus_{i = 1}^n a_i\)，然后将 \(c_i = a_i \oplus b_i\) 扔到线性基里面。我们可以发现，线性基最少数来拼出一个和 \(S\) 一样的数使得局面必输。那么，赢得概率就是 \(1 – (\frac12)^{siz}\)。
当然，如果拼不出来，那么就稳赢了。
Continue reading →BZOJ3590:「SNOI2013」Quare – 题解
主要思路
我操这个题是真的有意思（做完后索然无味）。
肯定这个题状压 DP 没跑的，所以可以先设 \(f[S]\) 为集合 \(S\) 双连通的最小代价。直接做有点困难，我们需要思考一个归纳的方式来构造一个双连通图。
Continue reading →AtCoder Grand Contest 038 – 解题报告
A – 01 Matrix
这个题还是很思博的，直接挂题解的图：
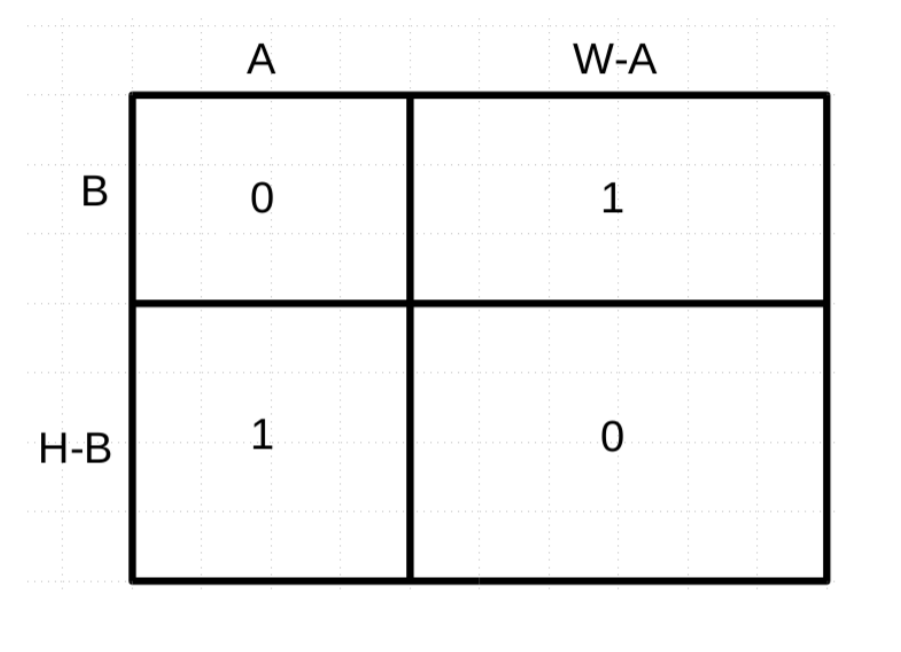
// A.cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, A, B;
scanf("%d%d%d%d", &n, &m, &B, &A);
for (int i = 1; i <= n; i++, puts(""))
for (int j = 1; j <= m; j++)
if ((i <= A) ^ (j <= B))
printf("1");
else
printf("0");
return 0;
}
// A.cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, A, B;
scanf("%d%d%d%d", &n, &m, &B, &A);
for (int i = 1; i <= n; i++, puts(""))
for (int j = 1; j <= m; j++)
if ((i <= A) ^ (j <= B))
printf("1");
else
printf("0");
return 0;
}
// A.cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, A, B;
scanf("%d%d%d%d", &n, &m, &B, &A);
for (int i = 1; i <= n; i++, puts(""))
for (int j = 1; j <= m; j++)
if ((i <= A) ^ (j <= B))
printf("1");
else
printf("0");
return 0;
}
Continue reading → AtCoder Grand Contest 041 – 解题报告
A – Table Tennis Training
思博题，考虑两端和奇偶性即可。
// A.cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n, A, B, ans = 0x7fffffffffffffff;
scanf("%lld%lld%lld", &n, &A, &B);
ans = min(A - 1, n - B) + 1 + ((B - A - 1) >> 1);
if (!((A^B) & 1))
ans = min(ans, (B - A) >> 1);
printf("%lld\n", ans);
return 0;
}
// A.cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n, A, B, ans = 0x7fffffffffffffff;
scanf("%lld%lld%lld", &n, &A, &B);
ans = min(A - 1, n - B) + 1 + ((B - A - 1) >> 1);
if (!((A^B) & 1))
ans = min(ans, (B - A) >> 1);
printf("%lld\n", ans);
return 0;
}
// A.cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n, A, B, ans = 0x7fffffffffffffff;
scanf("%lld%lld%lld", &n, &A, &B);
ans = min(A - 1, n - B) + 1 + ((B - A - 1) >> 1);
if (!((A^B) & 1))
ans = min(ans, (B - A) >> 1);
printf("%lld\n", ans);
return 0;
}
Continue reading → BZOJ2959:长跑 – 题解
主要思路
乍一看没办法维护图的最大点权和，但是注意到没有删边操作，且注意到一个双连通分量可以被缩点，所以我们可以用 LCT 来维护双连通分量。
考虑开两个并查集，一个是双连通分量的并查集，标号为 \(0\)；另外一个是维护连通性的并查集，标号为 \(1\)。
Continue reading →「Codeforces 461E」Appleman and a Game – 题解
主要思路
首先，不考虑原问题，只考虑最优策略，显然是当前能匹配的串越长越好。所以可以考虑二分答案，算当前拼接次数下能拼出来的最长的串，再将其与 \(n\) 进行比较。
Continue reading →