概述和基础概念

组合数学是 OI 中的一个重要考点。在开始讲解组合数学之前，我们先确立几个概念：

阶乘：一个正整数的阶乘为从1开始连续到这个数的乘积，记为\(n!\)。对于一个数的阶乘可以写作：
\[ n! = 1\times 2\times 3\times \dots \times n, n \in N^* \]

排列

排列(permutation)是用于解决下面这个问题而诞生的运算：

求从 n 个元素中取出 k 个元素，k 个元素的排列数量。

那么，我们可以把这个问题写作\( P_n^k \)。我们可以来推出这个问题的通解。首先确定范围，显然有\(k \leq n\)。之后，我们发现对于每一次取出元素的方案数与取出元素的次序有关，当我们第\(k\)次选取元素时，我们发现我们有\(n-k+1\)个选择；当我们第\(k-1\)次选取元素时，我们有\(n-k+2\)种选择…以此类推，通过乘法原理我们可以得出以下算式：

\[ P_n^k = n \times (n-1) \times (n-2) \times \dots \times (n-k+1) \]

通过我们上面介绍的阶乘，我们可以化简为：

\[ P_n^k = \frac{n!}{(n-k)!} \]

组合

组合其实是排列的“弱化版”。组合专注于解决这样的问题：

求从 n 个元素中取出有 k 个元素的集合，问集合的选取方案。

那么这就非常显然了，我们只需在排列问题上进行重复方案的消去即可。具体答案为：

\[ {n \choose k} = \frac{P_n^k}{k!} = \frac{n!}{(n-k)!k!} \]

插板法

插板法其实在高考数学中经常用到，我在这里简述一些经典问题便结束对插板法的表述。

例题把一行\(n\)个人划分成\(d\)组，试问有多少种方案。
解我们注意到\(n\)个人中有\(n-1\)个缝隙，可以把问题转换为\(n-1\)个缝隙中选\(d\)个的方案数，答案显然为\(n-1 \choose d\)。

斯特林数

第一类

还没学，弃坑。

第二类

例题：P1655:小朋友的球

斯特林数主要解决的问题是这样的：

第二类Stirling数是 n 个元素中定义 k 个等价类的方法数目。——Wikipedia

其递推公式为：

\[S(n, k) = S(n-1,k-1)+kS(n-1,k)\]

具体解释：递推关系的说明：考虑第n个物品，n可以单独构成一个非空集合，此时前n-1个物品构成k-1个非空的不可辨别的集合，有\(S(n-1,k-1)\)种方法；也可以前n-1种物品构成k个非空的不可辨别的集合，第n个物品放入任意一个中，这样有\(k*S(n-1,k)\)种方法。(src:Wikipedia)

例题代码：

# P1655.py
MAX_N = 405
stiring = [[0]*MAX_N for i in range(MAX_N)]
for i in range(1, MAX_N):
    stiring[i][i] = stiring[i][1] = 1
    for j in range(2, i):
        stiring[i][j] = stiring[i - 1][j - 1] + j * stiring[i - 1][j]
while True:
    try:
        n, m = map(int, input().split())
        print(stiring[n][m])
    except EOFError:
        break

错排问题

错排问题指的是这样一类问题：

设排列长度为\(n\)，问每个数都不在自己位置上的方案数为多少？

这个问题比较有趣。其递推式：

\[ D_n = nD_{n-1}+(-1)^n \]

这个数列可以解决很多问题，作者一时半会想不起来是洛谷上的哪道题，记起来之后会在此补充的。

卡特兰数

卡特兰数递推式为：

\[ Cat_n = \frac{2n \choose n}{n+1} \]

卡特兰数的意义为：

给定一个长度为\(n\)的序列，第\(i\)位\(0\)的前缀个数为\(zero[i]\)，\(1\)的前缀个数为\(one[i]\)。对于每一个\(i \leq n\)，都有\(zero[i] \geq one[i]\)。

以下几个问题都与卡特兰数有关：

合法的括号序列数量
\(n\)个节点的满二叉树数量
直角坐标系上从\((0,0)\)走到\((n,n)\)且不经过直线\(y=x\)的路径数量为\(2Cat_{n-1}\)。
\(n\)个元素的进出栈序列数量
\(Cat_n\)表示通过连结顶点而将\(n+2\)边的凸多边形分成三角形的方法个数。
\(Cat_n\)表示用\(n\)个长方形填充一个高度为\(n\)的阶梯状图形的方法个数。

卡特兰数的证明

在这里我们来证明为什么卡特兰数可以代表合法的括号序列数量。（下面证明思路来自于《组合数学》第 8 章第一节）

引理

长度为\(2n\)的合法括号序列的个数为\(Cat_n\)。

证明

我们把长度为\(2n\)的括号序列转化为一个由\(1, -1\)组成的序列，其中我们称合法的序列当且仅当\(\forall x \in [1, 2n], \sum_{i = 1}^x \geq 0\)，换句话讲，合法的序列的任何前缀的和都大于\(0\)。不满足以上条件的序列我们称其不合法的序列。显然，长度为\(2n\)的序列的方案数为合法序列和不合法序列方案数之和。我们定义长度为\(2n\)的合法序列的方案数为\(A_n\)，长度为\(2n\)的不合法序列的方案数为\(U_n\)。根据上面的论述，我们有：

\[ A_n + U_n = {2n \choose n} \]

我们的目标是计算\(A_n\)，我们可以考虑求出\(U_n\)来求它。考虑一个长度为\(2n\)的不合法序列\(a_1, a_2, \dots, a_{2n}\)，肯定存在一个最小的\(k\)：

\[ \sum_{i = 1}^k a_i < 0 \]

因为\(a_k\)的取值只有两种，且\(k\)是最小的，所以\(a_k = -1\)，\(\sum_{i = 1}^{k – 1} a_i = 0\)。我们还注意到\(k\)应该是奇数（请读者思考原因）。现在，我们这个序列前\(k\)个项每个值取反剩下不变，将前\(k\)个\(-1\)和\(1\)互换，那么变换后的序列包含\(n+1\)个\(+1\)和\(n-1\)个\(-1\)组成的序列。我们可以考虑映射计数（想要了解映射计数的读者可以参考这篇文章），即：存在第一个包含\(n+1\)个\(+1\)和\(n-1\)个\(-1\)组成的序列，也就是存在第一个\(+1\)个数超过\(-1\)个数的序列，所有符号取反之后也就意味着存在第一个\(-1\)个数超过\(+1\)个数的序列，也就是不合法序列。这两种序列是一一对应的。所以，\(U_n\)的取值等于第一个\(+1\)个数超过\(-1\)个数的序列的方案数：

\[ \frac{(2n)!}{(n+1)!(n-1)!} \]

然后带入原式相减之后，便是卡特兰数的最终结论了。

证明完毕。

多重集的排列组合

多重集的定义

多重集指的是每个类别的元素数量可能多于一个的集合，一般我们用下列符号表示：

\[S_m=\{ n_1*a_1, n_2*a_2, n_3*a_3, \dots, n_k*a_k \}\]

其中\(a_i\)指的是元素种类，\(n_i\)是第\(i\)类的元素个数。

多重集的组合问题

我们先考虑多重集组合数问题的弱化版：

若给定一个多重集\(S_m=\{ n_1*a_1, n_2*a_2, n_3*a_3, \dots, n_k*a_k \}\)，问取\(r\)个元素的方案是多少？（\(\forall i \in [1,k\, r\leq n_i]\)）。

那么这个问题很好解决，我们只要把这个问题转换为给定\(k-1\)个分割元素\(b\)和\(r\)个待选元素，求出其全排列方案数即可：

\[ k+r-1 \choose r \]

那么如果去掉\(\forall i \in [1,k\, r\leq n_]\)该如何求出呢？

我们可以考虑容斥原理，此时\(k+r-1 \choose r\)的意义是忽略掉元素限制的选法。容斥时，第一步我们先减去\(n_1+1\)个\(a_1\)的情况，也就是\(k+r-1-a_1-1 \choose r\)。然后我们再减去\(n_2+1\)个\(a_2\)的情况数，我们发现多减了一个部分：也就是这两个情况的交集，所以我们要加回来：\(+{k+r-1-a_1-1-a_2-1 \choose r}\)。根据容斥定理，最后结果为：

\[ {k+r-1 \choose r} – \sum_{i=1}^{k} {k+r-n_i-2 \choose r} + \sum_{i<j}^{k} {k+r-n_i-n_j-3 \choose r} – \dots \]

Prüfer 序列与无根树

正常情况下，一个无根树的表现形式大多都是图片或者是边的三元组集。现在我来介绍一种序列，可以与一棵无根树的形态对应，以便我们对其进行排列组合方面的探究。首先下图这棵树对应的 Prüfer 序列为：\(4,4,4,5\)。

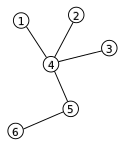
公有领域, https://commons.wikimedia.org/w/index.php?curid=592812

我来描述一下如何把一颗无根树转换为一个 Prufer 序列：

找到编号最小的叶子节点，删除它并把唯一与之相接的节点加入 Prufer 序列中。
重复第一个步骤，直到树只剩下两个节点。

我们可以发现，一个节点在 Prufer 序列中出现的次数是该节点的度减一，且这个序列的长度为\(n-2\)。所以，因为这两个性质，产生了一些公式。

引理1 节点个数为\(n\)的、形态不同的无根树有\(n^{n-2}\)种。

这个很好理解，把长度为\(n-2\)的 Prufer 序列对应到无根树上，排列组合可得。

引理2 如果给定点的个数\(n\)与每一个点的度数\(d_i\)，则不同形态的树有\(\frac{(n-2)!}{\prod_{i = 1}^n (d_i-1)!}\)种。

这个其实就是多重集的排列。长度为\(n-2\)的 Prufer 序列种存在\(d_i-1\)个的第\(i\)个点，我就不再赘述了。

引用

sources:

https://oi-wiki.org/math/stirling/
https://zh.wikipedia.org/wiki/%E9%94%99%E6%8E%92%E9%97%AE%E9%A2%98
https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0

OI 中的组合数学

目录