解法
这道题可以看作是网络流的一个模型了。我们把棋盘染色成红色和黑色。然后,源点连红色点,最大流限制为红点的点权;黑点全部连到汇点,最大流限制为黑点的点权。答案为点权总和减去最大流。
我们可以尝试理解一下:对于\(m = 1, n = 2\)的情况:
\[ [ x, y ] \]
那么假设\(x\)为黑点,\(y\)为红点,在网络上是这样的:
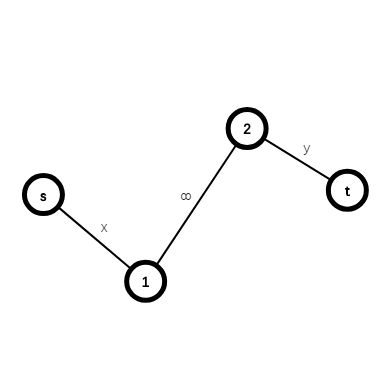
我们会发现最大流只会留下较小的一项。这样的话,我们可以感性推广到任何情况,大难点权和减掉最小割就行了。
代码
// LOJ6007.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 10003, INF = 0x3f3f3f3f;
const int vertical[4] = {0, 1, -1, 0}, hori[4] = {1, 0, 0, -1};
int n, m, sum, head[MAX_N], current, dep[MAX_N], s, t, cur[MAX_N];
int arr[50][50], color, colors[50][50];
struct edge
{
int to, nxt, weight;
} edges[80010];
void addpath(int src, int dst, int weight)
{
edges[current].to = dst, edges[current].nxt = head[src];
edges[current].weight = weight, head[src] = current++;
}
void add(int src, int dst, int weight)
{
addpath(src, dst, weight);
addpath(dst, src, 0);
}
bool bfs()
{
memset(dep, 0, sizeof(dep));
queue<int> q;
q.push(s), dep[s] = 1;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].weight > 0 && dep[edges[i].to] == 0)
{
dep[edges[i].to] = dep[u] + 1;
q.push(edges[i].to);
}
}
return dep[t] != 0;
}
int dfs(int u, int flow)
{
if (flow == 0 || u == t)
return flow;
for (int &i = cur[u]; i != -1; i = edges[i].nxt)
if (dep[edges[i].to] == dep[u] + 1 && edges[i].weight > 0)
if (int di = dfs(edges[i].to, min(flow, edges[i].weight)))
{
edges[i].weight -= di, edges[i ^ 1].weight += di;
return di;
}
return 0;
}
int dinic()
{
int ans = 0;
while (bfs())
{
for (int i = 0; i <= t; i++)
cur[i] = head[i];
while (int di = dfs(s, INF))
ans += di;
}
return ans;
}
int getPos(int x, int y) { return (x - 1) * m + y; }
int main()
{
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &m);
s = 0, t = n * m + 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &arr[i][j]), colors[i][j] = (i + j) & 1, sum += arr[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (colors[i][j] == 1)
add(getPos(i, j), t, arr[i][j]);
else
add(s, getPos(i, j), arr[i][j]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (colors[i][j] == 0)
for (int dir = 0; dir < 4; dir++)
{
int dstX = i + vertical[dir], dstY = j + hori[dir];
if (dstX > 0 && dstX <= n && dstY > 0 && dstY <= m)
add(getPos(i, j), getPos(dstX, dstY), INF);
}
int answer = sum - dinic();
printf("%d", answer);
return 0;
}