简述

Kruskal 重构树是图的一种生成树，主要解决一类路径边权限制问题。Kruskal 重构树有按深度单调的性质，所以很容易就可以解决边权的取值限制。

建法

Kruskal 重构树的建造方法和 Kruskal 算法建最小生成树的方法非常类似，但是结构有所不同：Kruskal 重构树将边权变成点权，点权依深度变小。我们假设有一张这样的图：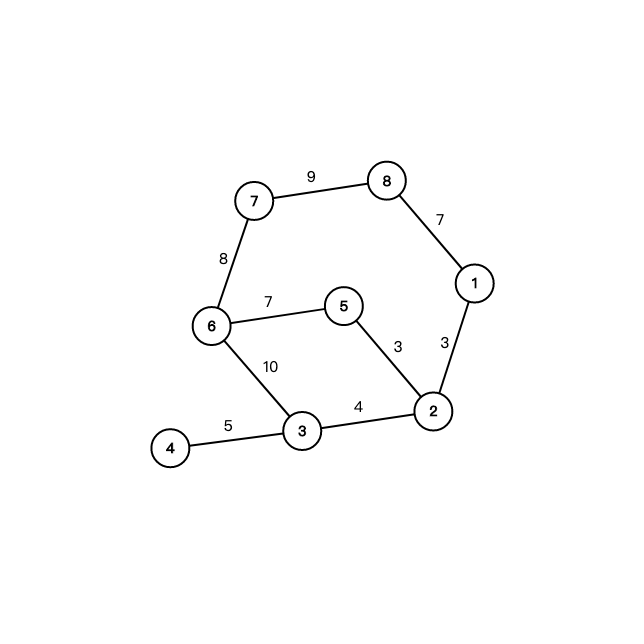

建重构树的时候，我们把所有的边都去掉：

然后我们按照边权大小从小到大进行遍历，发现最短边之后进行并查集查询，如果不在一个联通块内，那就新建一个节点，节点的点权为这条边的边权，然后这个新的节点连接两点，并成为整个大联通块的代表元素：

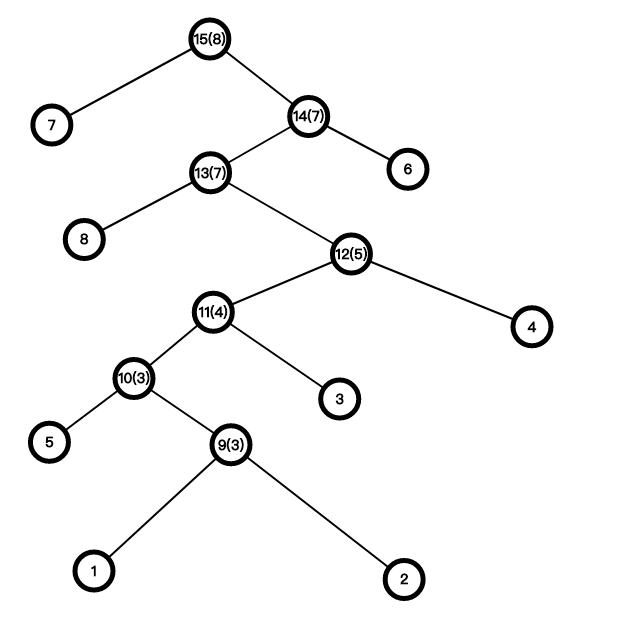
其中带括号的节点是重构树中新增的节点，括号内是他们的权值。我们发现随着深度的变小，权值在不严格单调地递增。这使得我们可以根据这个性质来满足题目中对边权大小的限制。

例题 A：P4197 Peaks

在Bytemountains有\(N\)座山峰，每座山峰有他的高度\(h_i\) 。有些山峰之间有双向道路相连，共\(M\)条路径，每条路径有一个困难值，这个值越大表示越难走，现在有\(Q\)组询问，每组询问询问从点\(v\)开始只经过困难值小于等于\(x\)的路径所能到达的山峰中第\(k\)高的山峰，如果无解输出\(-1\)。

这道题对路径有一个限制：路径上所有的边的边权都小于\(x\)，我们可以在 Kruskal 生成树上找到第一个点权小于\(x\)的节点，然后我们发现该子树内的点都满足这个条件。我们可以搞\(DFS\)序，然后权值主席树就可以搞定第\(k\)大问题。

// P4197.cpp
#include <bits/stdc++.h>
using namespace std;

const int MAX_N = 2e5 + 5, MAX_M = 5e5 + 5, MAX_T = 20 * MAX_N;

int head[MAX_N], current, fa[20][MAX_N], tot, n, m, q, hi[MAX_N], tmpx, tmpy, tmpz;
int buff[MAX_N], tmp[MAX_N], limit, pval[MAX_N], lft[MAX_N], rig[MAX_N], dfn;
int sum[MAX_T], lson[MAX_T], rson[MAX_T], roots[MAX_N], ttot;
struct edge
{
    int from, to, weight, nxt;
    bool operator<(const edge &e) const { return weight < e.weight; }
} G[MAX_M], edges[MAX_N];

void addpath(int src, int dst, int weight)
{
    edges[current].to = dst, edges[current].nxt = head[src];
    edges[current].from = src, edges[current].weight = weight;
    head[src] = current++;
}

int find(int x) { return (buff[x] == x) ? x : buff[x] = find(buff[x]); }

int update(int qx, int l, int r, int pre)
{
    int p = ++ttot;
    sum[p] = sum[pre] + 1;
    if (l == r)
        return p;
    int mid = (l + r) >> 1;
    rson[p] = rson[pre], lson[p] = lson[pre];
    if (qx <= mid)
        lson[p] = update(qx, l, mid, lson[pre]);
    else
        rson[p] = update(qx, mid + 1, r, rson[pre]);
    return p;
}

int query(int a, int x, int k)
{
    int l = 1, r = limit;
    for (int i = 19; i >= 0; i--)
        if (fa[i][a] != 0 && pval[fa[i][a]] <= x)
            a = fa[i][a];
    int v = roots[rig[a]], u = roots[lft[a] - 1];
    if (sum[v] - sum[u] < k)
        return -1;
    while (l < r)
    {
        int tp = sum[rson[v]] - sum[rson[u]], mid = (l + r) >> 1;
        if (tp >= k)
            v = rson[v], u = rson[u], l = mid + 1;
        else
            v = lson[v], u = lson[u], r = mid, k -= tp;
    }
    return tmp[r];
}

void dfs(int u)
{
    for (int i = 1; i < 20; i++)
        fa[i][u] = fa[i - 1][fa[i - 1][u]];
    lft[u] = ++tot;
    if (u <= n)
        roots[tot] = update(hi[u], 1, limit, roots[tot - 1]);
    else
        roots[tot] = roots[tot - 1];
    for (int i = head[u]; i != -1; i = edges[i].nxt)
        dfs(edges[i].to);
    rig[u] = tot;
}

int main()
{
    memset(head, -1, sizeof(head));
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= 2 * n; i++)
        buff[i] = i;

    for (int i = 1; i <= n; i++)
        scanf("%d", &hi[i]), tmp[i] = hi[i];
    for (int i = 1; i <= m; i++)
        scanf("%d%d%d", &tmpx, &tmpy, &tmpz), G[i] = edge{tmpx, tmpy, tmpz, -1};

    sort(tmp + 1, tmp + 1 + n), limit = unique(tmp + 1, tmp + 1 + n) - tmp - 1;
    for (int i = 1; i <= n; i++)
        hi[i] = lower_bound(tmp + 1, tmp + 1 + limit, hi[i]) - tmp;

    dfn = n, sort(G + 1, G + 1 + m);

    for (int i = 1; i <= m; i++)
    {
        int a = find(G[i].from), b = find(G[i].to);
        if (a != b)
        {
            pval[++dfn] = G[i].weight, buff[a] = buff[b] = dfn;
            addpath(dfn, a, 0), addpath(dfn, b, 0);
            fa[0][a] = fa[0][b] = dfn;
            if (dfn - n == n - 1)
                break;
        }
    }

    for (int i = 1; i <= dfn; i++)
        if (lft[i] == 0)
            dfs(find(i));

    while (q--)
    {
        int v, x, k;
        scanf("%d%d%d", &v, &x, &k), printf("%d\n", query(v, x, k));
    }
    return 0;
}

例题 B：P4768 [NOI2018]归程

这道题其实也是一道 Kruskal 重构树傻逼题。我们考虑给每一组图先跑一个最短路（注意本题卡 SPFA），然后建立一个 Kruskal 重构树（按海拔从大到小进行排序）。考虑用倍增找到点权最接近询问的点，然后在其子树内寻找最短路最短的点即可。最短路最短的点可以预先用一遍 DFS 搞定。整个预处理的时间复杂度是\(O(n \log n)\)，整个复杂度是\(O(T * n \log n)\)。

// P4768.cpp
#include <bits/stdc++.h>
#define pr pair<int, int>
using namespace std;

const int MAX_N = 4e5 + 2000, MAX_M = 4e5 + 2000, INF = 0x3f3f3f3f;

int T, n, m;
int head_graph[MAX_N], head_tree[MAX_N], current_graph, current_tree, buff[MAX_N];
int ptot, fa[20][MAX_N], val[MAX_N], smallest[MAX_N], dist[MAX_N];
bool vis[MAX_N];

struct edge
{
    int from, to, nxt, weight, height;
    bool operator<(const edge &e) const { return height > e.height; }
} source[MAX_M], edges[MAX_M << 1], tree[MAX_N];

int find(int x) { return x == buff[x] ? x : buff[x] = find(buff[x]); }

void addpath(int src, int dst, int weight, int height)
{
    edges[current_graph].to = dst, edges[current_graph].height = height;
    edges[current_graph].nxt = head_graph[src], edges[current_graph].weight = weight;
    head_graph[src] = current_graph++;
}

void addbranch(int src, int dst)
{
    tree[current_tree].to = dst, tree[current_tree].nxt = head_tree[src];
    head_tree[src] = current_tree++;
}

void djisktra()
{
    memset(dist, 0x3f, sizeof(dist)), memset(vis, false, sizeof(vis));
    priority_queue<pr> pq;
    pq.push(make_pair(0, 1)), dist[1] = 0;
    while (!pq.empty())
    {
        int u = pq.top().second;
        pq.pop();
        if (vis[u])
            continue;
        vis[u] = true;
        for (int i = head_graph[u]; i != -1; i = edges[i].nxt)
            if (!vis[edges[i].to] && dist[edges[i].to] > dist[u] + edges[i].weight)
                dist[edges[i].to] = dist[u] + edges[i].weight, pq.push(make_pair(-dist[edges[i].to], edges[i].to));
    }
}

void dfs(int u)
{
    smallest[u] = 0;
    if (u <= n)
        smallest[u] = u;
    for (int i = 1; i < 20; i++)
        fa[i][u] = fa[i - 1][fa[i - 1][u]];
    for (int i = head_tree[u]; i != -1; i = tree[i].nxt)
    {
        fa[0][tree[i].to] = u, dfs(tree[i].to);
        if (dist[smallest[u]] > dist[smallest[tree[i].to]])
            smallest[u] = smallest[tree[i].to];
    }
}

void kruskal()
{
    sort(source + 1, source + 1 + m);
    for (int i = 1; i <= m; i++)
    {
        int a = find(source[i].from), b = find(source[i].to);
        if (a != b)
        {
            int p = ++ptot;
            buff[a] = buff[b] = buff[p] = p, val[p] = source[i].height;
            fa[0][a] = fa[0][b] = p;
            addbranch(p, a), addbranch(p, b);
        }
    }
    dist[0] = INF, dfs(ptot);
}

int find_smallest(int u, int limit)
{
    for (int i = 19; i >= 0; i--)
        if (fa[i][u] && val[fa[i][u]] > limit)
            u = fa[i][u];
    return u;
}

int main()
{
    scanf("%d", &T);
    while (T--)
    {
        scanf("%d%d", &n, &m);
        memset(head_graph, -1, sizeof(head_graph)), memset(head_tree, -1, sizeof(head_tree));
        current_graph = current_tree = 0, ptot = n;
        memset(fa, 0, sizeof(fa)), memset(val, 0, sizeof(val)), memset(smallest, 0, sizeof(smallest));
        for (int i = 1; i <= 2 * n; i++)
            buff[i] = i;
        for (int i = 1; i <= m; i++)
        {
            scanf("%d%d%d%d", &source[i].from, &source[i].to, &source[i].weight, &source[i].height);
            addpath(source[i].from, source[i].to, source[i].weight, source[i].height);
            addpath(source[i].to, source[i].from, source[i].weight, source[i].height);
        }
        djisktra(), kruskal();
        int lastans = 0, q, k, s;
        scanf("%d%d%d", &q, &k, &s);
        while (q--)
        {
            int v, p;
            scanf("%d%d", &v, &p), v = (v + k * lastans - 1) % n + 1, p = (p + k * lastans) % (s + 1);
            int ans = find_smallest(v, p);
            printf("%d\n", lastans = dist[smallest[ans]]);
        }
    }
    return 0;
}