今天比赛状态极差,又困、又饿,眼睛又干。
A – 拯救奶牛
我们先把问题转换为三角矩阵上两点的距离,可以类比曼哈顿距离,我们可以把距离分为纵向和横向两种来考虑。
首先是纵向。如果\((x_1,y_1)\)要到\((x_2,y_2)\),那么分下面几种情况:
- 如果\(x_1\)和\(x_2\)的奇偶性不同,那么贡献为\(2|x_1-x_2|-1\)。
- 如果相同,那么贡献为\(2|x_1-x_2|\)。
那么再来看横向。我们发现,如果我们把上方的三角形扩大成这样:
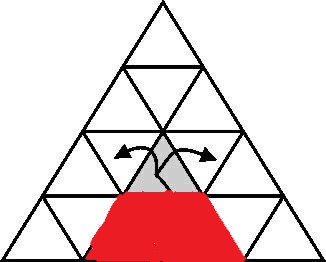
我们发现,这一范围内的三角形不需要额外的横向贡献,只需要计算纵向贡献即为答案。对于在同一行却不在这个区域内的三角形,横向贡献也非常好计算,做差乘二即可。
记得要对输入点进行排序。
代码
// A.cpp
#include <bits/stdc++.h>
#define pr pair<int, int>
using namespace std;
const int MAX_N = 1001000;
pr prs[MAX_N];
int n, m, si, sj;
int answer, exitI, exitJ;
int main()
{
answer = 0x3f3f3f3f;
scanf("%d%d%d%d", &m, &n, &si, &sj);
for (int i = 1; i <= n; i++)
scanf("%d%d", &prs[i].first, &prs[i].second);
sort(prs + 1, prs + 1 + n);
for (int i = 1; i <= n; i++)
{
pr pta = prs[i], ptb = make_pair(si, sj);
if (pta.first < ptb.first)
swap(pta, ptb);
int jl = ptb.second, jr = ptb.second + (pta.first - ptb.first) * 2;
int ans = (pta.first - ptb.first) << 1;
if (pta.second >= jl && pta.second <= jr &&
(ans < answer || (ans == answer && exitJ >= prs[i].second)))
{
answer = ans, exitI = prs[i].first, exitJ = prs[i].second;
if ((pta.second & 1) != (ptb.second & 1))
answer -= 1;
continue;
}
ans += min(abs(pta.second - jl), abs(pta.second - jr));
if (ans < answer || (ans == answer && exitJ >= prs[i].second))
answer = ans, exitI = prs[i].first, exitJ = prs[i].second;
}
printf("%d %d\n%d", exitI, exitJ, answer + 1);
return 0;
}
B – 邮递员
首先,这道题的\(w_i\)毫无卵用。我们来看这个\(w_i\)对亏损的贡献:
\[ \sum_{i=1}^{n}( i-w_{s_i} )= \frac{n(n-1)}{2}-\sum_{i=1}^{n} w_i \]
所以顺序根本不会造成影响。所以,我们来找一条最短的一笔画路径且字典序最小,方可保证答案最简。
因为题目里明显的说了(可惜我没看到,眼瞎了)
能够离开每个村子的路口的数目一定是2,4或者8。
我可真是个傻逼。
所以,用邻接表存图,然后按标号从小到大进行 DFS 写栈,最后反向弹栈输出即可。
代码
// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 220;
int n, m, wi[MAX_N], tmpx, tmpy, dist[MAX_N][MAX_N], tot;
stack<int> stk;
void dfs(int u)
{
for (int i = 1; i <= n; i++)
if (dist[u][i])
{
dist[u][i]--, dist[i][u]--;
dfs(i);
}
stk.push(u);
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &wi[i]);
for (int i = 1; i <= m; i++)
scanf("%d%d", &tmpx, &tmpy), dist[tmpx][tmpy]++, dist[tmpy][tmpx]++;
dfs(1);
printf("%d\n", stk.size() - 1);
while (!stk.empty())
printf("%d ", stk.top()), stk.pop();
return 0;
}
C – 最小密度路径
我们可以考虑设置状态\(f[i][j][k]\)为从节点\(i\)到\(j\)走了\(k\)条边的总长度,然后 Floyd 预处理,最后\(O(n)\)回答即可,傻逼题。
代码
// C.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 55, MAX_M = 1200;
int n, m, tmpx, tmpy, tmpz, f[MAX_N][MAX_N][MAX_M], dist[MAX_N][MAX_N], q;
int main()
{
scanf("%d%d", &n, &m);
memset(f, 0x3f, sizeof(f)), memset(dist, 0x3f, sizeof(dist));
for (int i = 1; i <= m; i++)
scanf("%d%d%d", &tmpx, &tmpy, &tmpz), dist[tmpx][tmpy] = min(dist[tmpx][tmpy], tmpz);
for (int i = 1; i <= n; i++)
f[i][i][0] = 0;
for (int s = 1; s <= n; s++)
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (f[i][j][s] > f[i][k][s - 1] + dist[k][j])
f[i][j][s] = f[i][k][s - 1] + dist[k][j];
scanf("%d", &q);
while (q--)
{
double ans = (double)0x3f3f3f3f;
int i, j;
bool flag = true;
scanf("%d%d", &i, &j);
for (int s = 1; s <= n; s++)
if (1.0 * f[i][j][s] / (1.0 * s) < ans && f[i][j][s] != (double)0x3f3f3f3f)
ans = min(ans, 1.0 * f[i][j][s] / (1.0 * s)), flag = false;
if (flag)
puts("OMG!");
else
printf("%.3lf\n", ans);
}
return 0;
}