CH2601:电路维修题解

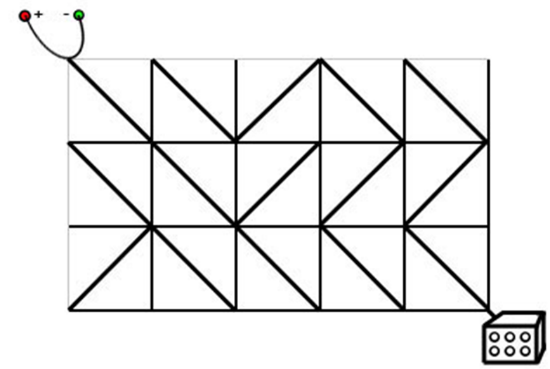
思路

我们可以把整个电路系统想成是一个无向图，如果从点\(A(x_1,y_1)到B(x_2,y_2)\)且这个路上的方格的电路时符合走向的，那么认定这条路的边权为\(0\)，如果与走向相悖，那么边权为\(1\)。为了做一个合理的优化，我们可以使用双端队列，优先处理边权为\(0\)的边，然后确保每个点只经过一次即可。复杂度比较低，看代码吧。

// CH2601.cpp
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
#define pr pair<int, int>
#define ppr pair<int, pr>
using namespace std;
const int maxn = 510, dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1}, INF = 0x3f3f3f3f;
const char sym[4] = {'\\', '/', '\\', '/'};
int T, N, M, dist[maxn][maxn];
char map[maxn][maxn];
bool validiate(int x, int y) { return x > 0 && x <= N + 1 && y > 0 && y <= M + 1; }
int main()
{
    scanf("%d", &T);
    while (T--)
    {
        memset(dist, 0x3f, sizeof(dist));
        scanf("%d%d", &N, &M);
        for (int i = 1; i <= N; i++)
            scanf("%s", map[i] + 1);
        deque<ppr> qpool;
        qpool.push_back(make_pair(0, make_pair(1, 1)));
        while (!qpool.empty())
        {
            ppr curt = qpool.front();
            int x = curt.second.first, y = curt.second.second, k = curt.first;
            qpool.pop_front();
            if (dist[x][y] != INF)
                continue;
            dist[x][y] = k;
            for (int i = 0; i < 4; i++)
            {
                int a = x + dx[i], b = y + dy[i];
                if (validiate(a, b) && dist[a][b] == INF)
                {
                    if (sym[i] == map[min(a, x)][min(b, y)])
                        qpool.push_front(make_pair(k, make_pair(a, b)));
                    else
                        qpool.push_back(make_pair(k + 1, make_pair(a, b)));
                }
            }
        }
        if (dist[N][M] == INF)
            printf("NO SOLUTION\n");
        else
            printf("%d\n", dist[N + 1][M + 1]);
    }
    return 0;
}