A – 01 Matrix
这个题还是很思博的,直接挂题解的图:
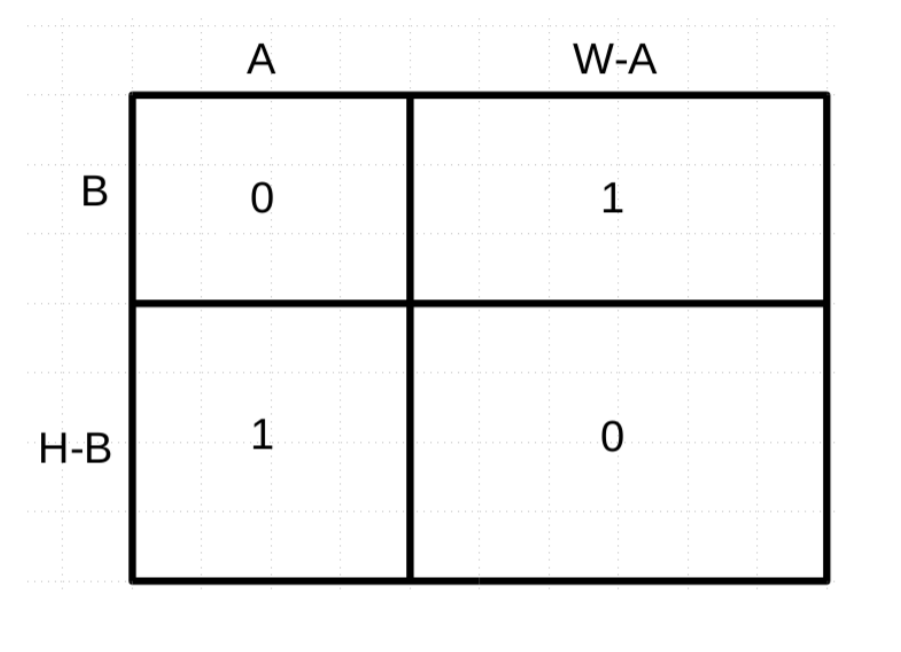
// A.cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, A, B;
scanf("%d%d%d%d", &n, &m, &B, &A);
for (int i = 1; i <= n; i++, puts(""))
for (int j = 1; j <= m; j++)
if ((i <= A) ^ (j <= B))
printf("1");
else
printf("0");
return 0;
}
B – Sorting a Segment
这个题姑且有点意思。首先答案上限是 \(n – k + 1\),然后我们可以思考两个区间的排序效果是否相同。有两种情况:
- 第一种情况是两个区间并不相交,那么排序效果相同的充要条件就是这两个区间都是单调不降的。这个东西用 ST 表可以轻松维护。
- 第二种情况是两个区间相交,有 \(l_1 < l_2 < r_1 < l_2\)。那么对于 \([l_1, l_2), (r_1, l_2]\) 这两个区间,需要满足单调不降;对于 \([l_2, r_1]\) 而言,其最小值需要不小于 \([l_1, l_2)\) 的最大值、其最大值需要不大于 \((r_1, l_2]\) 的最小值。满足这些条件,显然排序效果相同。
可以观察出一个结论,如果两个区间 \([i, i + k – 1], [j, j + k – 1], i < j\) 满足效果相同,那么 \([i, i + k – 1]\) 与 \([x, x + k – 1], x \in [i, j]\) 是效果相同的。知道这个结论之后可以直接 \(\Theta(n)\) 扫。
当然还要注意整个区间都是单调不降的情况。
// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 2e5 + 200;
int n, k, pi[MAX_N], max_val[20][MAX_N], min_val[20][MAX_N], log2_[MAX_N];
bool st[20][MAX_N];
bool query(int l, int r)
{
bool ret = true;
for (int i = 19; i >= 0; i--)
if (l + (1 << i) - 1 <= r)
{
ret &= st[i][l] && (l + (1 << i) - 1 == r || pi[l + (1 << i) - 1] <= pi[l + (1 << i)]);
l += (1 << i);
}
return ret;
}
int queryMin(int l, int r)
{
int d = log2_[r - l + 1];
return min(min_val[d][l], min_val[d][r - (1 << d) + 1]);
}
int queryMax(int l, int r)
{
int d = log2_[r - l + 1];
return max(max_val[d][l], max_val[d][r - (1 << d) + 1]);
}
int main()
{
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++)
scanf("%d", &pi[i]), st[0][i] = true, max_val[0][i] = min_val[0][i] = pi[i];
for (int i = 2; i <= n; i++)
log2_[i] = log2_[i >> 1] + 1;
for (int i = 1; i < 20; i++)
for (int j = 1; j + (1 << i) - 1 <= n; j++)
{
st[i][j] = st[i - 1][j] && st[i - 1][j + (1 << (i - 1))] && (pi[j + (1 << (i - 1)) - 1] <= pi[j + (1 << (i - 1))]);
min_val[i][j] = min(min_val[i - 1][j], min_val[i - 1][j + (1 << (i - 1))]);
max_val[i][j] = max(max_val[i - 1][j], max_val[i - 1][j + (1 << (i - 1))]);
}
int pl = -1, pr = -1, ans = 0;
bool flag = false;
for (int i = 1; i + k - 1 <= n; i++)
if (pl == -1)
ans++, pl = i, pr = i + k - 1, flag |= query(pl, pr);
else if (i <= pr)
{
bool verdict = query(pl, i - 1) && query(pr + 1, i + k - 1);
verdict &= queryMax(pl, i - 1) <= queryMin(i, pr) && queryMax(i, pr) <= queryMin(pr + 1, i + k - 1);
if (verdict)
continue;
else if (!(query(i, i + k - 1) && flag))
ans++, pl = i, pr = i + k - 1, flag |= query(pl, pr);
}
else if (query(pl, pr) && query(i, i + k - 1))
continue;
else if (!(query(i, i + k - 1) && flag))
ans++, pl = i, pr = i + k - 1, flag |= query(pl, pr);
printf("%d\n", ans);
return 0;
}
C – LCMs
题解的方法很奇怪,我在这里翻译一下。
我们设一个 \(\sum_{d | x} c_d = \frac{1}{x}\),这个原本的 \(c_i\) 可以用 \(\Theta(n \log n)\) 随便算算即可。
考虑原式展开:
\[ \sum_{i = 1}^{n – 1} \sum_{j = i + 1}^n \frac{a_i a_j}{\gcd(a_i, a_j)} = \sum_{i = 1}^{n – 1} \sum_{j = i + 1}^n a_i a_j \sum_{d|i, d|j} c_d \]
换下顺序:
\[ \sum_{d = 1}^{upper} c_d \sum_{i = 1}^{n – 1} \sum_{j = i + 1}^n a_i a_j [d | a_i] [d | a_j] \]
埃筛走一波直接完事。
// C.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e6 + 200, mod = 998244353;
int n, upper, ai[MAX_N], bi[MAX_N], ci[MAX_N];
int fpow(int bas, int tim)
{
int ret = 1;
while (tim)
{
if (tim & 1)
ret = 1LL * ret * bas % mod;
bas = 1LL * bas * bas % mod;
tim >>= 1;
}
return ret;
}
const int inv2 = fpow(2, mod - 2);
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &ai[i]), bi[ai[i]]++;
upper = *max_element(ai + 1, ai + 1 + n);
for (int i = 1; i <= upper; i++)
ci[i] = fpow(i, mod - 2);
for (int i = 1; i <= upper; i++)
for (int j = (i << 1); j <= upper; j += i)
ci[j] = (0LL + ci[j] + mod - ci[i]) % mod;
int ans = 0;
for (int d = 1; d <= upper; d++)
{
int p1 = 0, p2 = 0;
for (int i = d; i <= upper; i += d)
p1 = (0LL + p1 + 1LL * bi[i] * i % mod) % mod, p2 = (0LL + p2 + 1LL * bi[i] * i % mod * i % mod) % mod;
int pans = (0LL + 1LL * p1 * p1 % mod + mod - p2) % mod * inv2 % mod;
ans = (0LL + ans + 1LL * pans * ci[d] % mod) % mod;
}
printf("%d\n", ans);
return 0;
}
D – Unique Path
这个题可以大概知道一个思路:首先这个形态是一个若干双连通分量组成的树,那么在可以乱搞的情况下,判断 YES 和 NO 的唯一标准就是 \(m\) 是否在制定的范围之内。我们需要算边的下限和上限。当然,非法的情况需要我们提前判掉。
我们可以对 \(0\) 的询问建并查集。首先,如果 \(1\) 的两个点是否在一个连通块内,那么肯定非法,这个显然。
这个并查集的反图就是我们要求的那个合法图,显然是一一对应的。我们可以对团进行 \({k \choose 2}\) 的累积,然后算出答案区间。
// D.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e5 + 200;
int n, m, q, mem[MAX_N], siz[MAX_N];
struct clue
{
int a, b, c;
} clues[MAX_N];
int find(int x) { return mem[x] == x ? x : mem[x] = find(mem[x]); }
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i++)
mem[i] = i;
for (int i = 1; i <= q; i++)
{
scanf("%d%d%d", &clues[i].a, &clues[i].b, &clues[i].c);
clues[i].a++, clues[i].b++;
if (clues[i].c == 0 && find(clues[i].a) != find(clues[i].b))
mem[find(clues[i].a)] = find(clues[i].b);
}
int component = 0, c1 = 0;
for (int i = 1; i <= n; i++)
component += find(i) == i;
for (int i = 1; i <= q; i++)
if (clues[i].c == 1)
{
c1++;
int u = find(clues[i].a), v = find(clues[i].b);
if (u == v)
puts("No"), exit(0);
}
long long lft = c1 ? max(3, component) : component - 1, rig = 1LL * component * (component - 1) / 2;
puts((lft <= m - (n - component) && m - (n - component) <= rig) ? "Yes" : "No");
return 0;
}
E – Gachapon
来到最有意思的一个题了。
首先我们清楚,本题求的是全集均满足 \(x_i \geq b_i\) 的期望次数。那么,通过 min-max 反演,可以转换成求至少有一个满足 \(x_i \geq b_i\) 的期望次数。
那么我们计算这个东西,由于期望的线性性,『至少有一个满足 \(x_i \geq b_i\) 的期望次数』等于『局面 \((x_1, x_2, x_3, \dots, x_n), \forall x_i < b_i\) 的期望次数之和乘上其概率』。
我知道这个东西很玄学,我花了很久的时间弄懂这个东西(不过如此)。
我们考虑把每个局面 \((x_1, x_2, x_3, \dots, x_n)\) 抽象成 DAG 的一个点,显然起点是全零局面、终止节点是 \((x_1, x_2, x_3, \dots, x_n), \exists x_i = b_i\),这个终止节点我们可以通过加一个虚点来承接这些点的转移。局面之间的边为局面之间的转变,赋其权为顺利经过其的期望次数。显然到虚点的边权为 \(0\)。
那么我们的目标是算出 \(E(S \to T)\)。正常来讲,可以考虑用 DAG 上的 DP 进行计算。我们可以把概率和期望列出来,算出:
\[ (f(u) + w(u, v)) \times P(S \to u) \times P(u \to v) \to f(v) \]
然而我们并不需要建图来搞,可以考虑直接对每个边算贡献。
\[ prod = P(S \to u) P(u \to v) P(v \to T) w(u, v) \]
首先,这个 \(P(v \to T)\) 就很傻逼,因为所有方式都能到达 \(T\),所以 \(P(v \to T) = 1\)。
\[ prod = P(S \to u) P(u \to v) w(u, v) \]
看上去已经很难算了。我们考虑对一个点 \(u\) 打包来算 \(G(u) = \sum_{(u, v) \in E} P(u \to v) w(u, v)\)。
这个怎么算?其实考虑 \(G(u)\) 的含义其实就是跳出本状态的期望次数。那么:
\[ G(u) = \frac{\sum_{i \in u} a_i }{\sum a_i} \times 1 + (1 – \frac{\sum_{i \in u} a_i }{\sum a_i}) \times (G(u) + 1) \]
得:
\[ G(u) = \frac{\sum a_i }{\sum_{i \in u} a_i} \]
这个搞定,回到刚刚计算贡献的部分:
\[ prod_u = P(S \to u) G(u) \]
现在需要计算 \(P(S \to u)\),这个也很简单,考虑一个随机数的输出序列,然后算出来:
\[ P(S \to u) = \frac{(\sum x_i)!}{\prod_{i \in u} x_i !} \prod_{i \in u} (\frac{a_i}{\sum_{j \in u} a_j})^{x_i} \]
所以最后的单贡献是:
\[ prod = \sum_{u} (\sum a_i) \times (\sum x_i)! (\frac{1}{\sum_{i \in u} a_i})^{1 + \sum x_i} \prod_{i \in u} \frac{a_i^{x_i}}{x_i!} \]
这个东西可以做背包 DP,然后每次转移的时候记得加上 min-max 反演的符号即可。
// E.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 440, mod = 998244353;
int n, ai[MAX_N], bi[MAX_N], sa, sb, inv[MAX_N], fac[MAX_N], dp[2][MAX_N][MAX_N];
int fpow(int bas, int tim)
{
int ret = 1;
while (tim)
{
if (tim & 1)
ret = 1LL * ret * bas % mod;
bas = 1LL * bas * bas % mod;
tim >>= 1;
}
return ret;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d%d", &ai[i], &bi[i]), sa += ai[i], sb += bi[i];
inv[0] = inv[1] = 1;
for (int i = 2; i < MAX_N; i++)
inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod;
for (int i = fac[0] = 1; i < MAX_N; i++)
fac[i] = 1LL * fac[i - 1] * i % mod;
for (int i = 1; i < MAX_N; i++)
inv[i] = 1LL * inv[i] * inv[i - 1] %
int b = 0;
dp[0][0][0] = mod - 1;
for (int i = 1; i <= n; i++)
{
b ^= 1;
for (int s = 0; s <= sa; s++)
for (int c = 0; c <= sb; c++)
{
dp[b][s][c] = dp[!b][s][c];
if (s < ai[i])
continue;
for (int idx = 0, acc = 1; idx < bi[i] && idx <= c; idx++, acc = 1LL * acc * ai[i] % mod)
dp[b][s][c] = (0LL + dp[b][s][c] + mod - 1LL * acc * inv[idx] % mod * dp[!b][s - ai[i]][c - idx] % mod) % mod;
}
}
int ans = 0;
for (int s = 0; s <= sa; s++)
{
int unit = fpow(s, mod - 2);
for (int idx = 0, acc = unit; idx <= sb; idx++, acc = 1LL * acc * unit % mod)
ans = (0LL + ans + 1LL * fac[idx] * acc % mod * dp[b][s][idx] % mod) % mod;
}
ans = 1LL * ans * sa % mod, printf("%d\n", ans);
return 0;
}