AtCoder Grand Contest 035 – 解题报告

A – XOR Circle

考虑对仅有的 \(s \leq 3\) 个元素排列顺序然后判就完事了。

// A.cpp
#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 1e5 + 200;

int n, ai[MAX_N], si[MAX_N];
map<int, int> mp, tmp;

int main()
{
    scanf("%d", &n);
    for (int i = 1, x; i <= n; i++)
        scanf("%d", &ai[i]), mp[ai[i]]++;
    if (mp.size() <= 3)
    {
        vector<int> vi;
        for (auto x : mp)
            vi.push_back(x.first);
        bool flag = false;
        do
        {
            int len = vi.size();
            tmp.clear();
            for (int i = 1; i <= 2; i++)
                si[i] = vi[(i - 1) % len];
            for (int i = 3; i <= n; i++)
                si[i] = si[i - 1] ^ si[i - 2];
            for (int i = 1; i <= n; i++)
                tmp[si[i]]++;
            bool cflag = true;
            for (auto x : tmp)
                cflag &= mp[x.first] == x.second;
            flag |= cflag;
        } while (next_permutation(vi.begin(), vi.end()));
        puts(flag ? "Yes" : "No");
    }
    else
        puts("No");
    return 0;
}

B – Even Degrees

套路题，首先搞出一个 DFS 树，然后贪心的尝试让本子树合法即可，因为当本子树对子树根的父节点产生影响时，也会存在一个返回父亲的边对其进行调整。当然，调整到根还不行那肯定无解了。

// B.cpp
#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 1e5 + 200;

typedef pair<int, int> pii;

int n, m, head[MAX_N], current, parity[MAX_N];
bool inst[MAX_N], vis[MAX_N];
vector<pii> ansBox;

struct edge
{
    int to, nxt;
} edges[MAX_N << 1];

void addpath(int src, int dst)
{
    edges[current].to = dst, edges[current].nxt = head[src];
    head[src] = current++;
}

bool dfs(int u, int fa)
{
    vis[u] = inst[u] = true;
    for (int i = head[u]; i != -1; i = edges[i].nxt)
        if (!vis[edges[i].to] && edges[i].to != fa)
        {
            bool res = dfs(edges[i].to, u);
            parity[u] ^= !res;
            if (res)
                ansBox.push_back(make_pair(edges[i].to, u));
            else
                ansBox.push_back(make_pair(u, edges[i].to));
        }
    inst[u] = false;
    for (int i = head[u]; i != -1; i = edges[i].nxt)
        if (inst[edges[i].to] && edges[i].to != fa)
            if (parity[u])
                parity[u] ^= 1, ansBox.push_back(make_pair(u, edges[i].to));
            else
                parity[edges[i].to] ^= 1, ansBox.push_back(make_pair(edges[i].to, u));
    return parity[u];
}

int main()
{
    memset(head, -1, sizeof(head));
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; i++)
        scanf("%d%d", &u, &v), addpath(u, v), addpath(v, u);
    if (!dfs(1, 0))
        for (pii x : ansBox)
            printf("%d %d\n", x.first, x.second);
    else
        puts("-1");
    return 0;
}

C – Skolem XOR Tree

先参考下面的图：

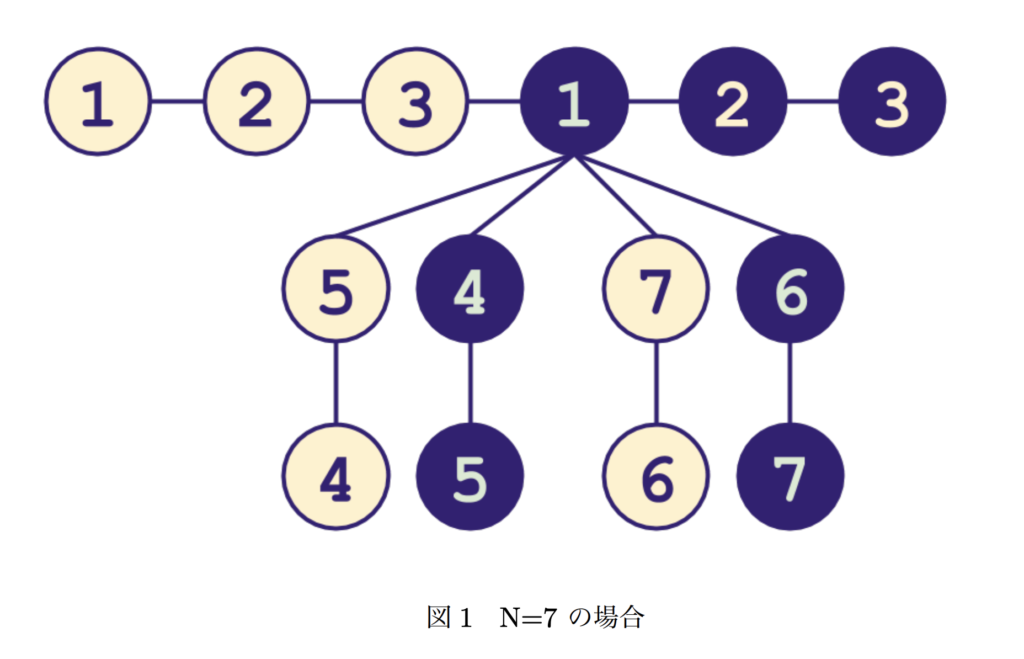
考虑一个 \(2i \oplus (2i + 1) = 1\) 性质，所以可以直接这样去搞。

如果 \(n\) 是偶数的话，就只能搞出来一条半链，所以我们考虑直接枚举整链的接点，强心接上去即可。

// C.cpp
#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 1e5 + 200;

int n;

int main()
{
    scanf("%d", &n);
    if (__builtin_popcount(n) == 1)
        puts("No"), exit(0);
    puts("Yes"), printf("1 2\n2 3\n3 %d\n%d %d\n%d %d\n", n + 1, n + 1, n + 2, n + 2, n + 3);
    for (int i = 4; i < n; i += 2)
        printf("1 %d\n%d %d\n1 %d\n%d %d\n", i, i, i + 1 + n, i + 1, i + 1, i + n);
    if (!(n & 1))
    {
        for (int i = 2; i <= n; i++)
        {
            int u = i ^ n ^ 1;
            if (i != 3 && u != 3 && u <= n)
            {
                printf("%d %d\n%d %d\n", i, n, u, 2 * n);
                break;
            }
        }
    }
    return 0;
}

D – Add and Remove

直接搜。

// D.cpp
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll MAX_N = 20, INF = 0x3f3f3f3f3f3f3f3f;

int n;
ll ai[MAX_N];

ll solve(int l, int r, ll cL, ll cR)
{
    if (l + 1 > r - 1)
        return 0;
    ll ret = INF;
    for (int i = l + 1; i <= r - 1; i++)
        ret = min(ret, solve(l, i, cL + cR, cR) + solve(i, r, cL, cL + cR) + 1LL * (cL + cR) * ai[i]);
    return ret;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &ai[i]);
    printf("%lld\n", solve(1, n, 1, 1) + ai[1] + ai[n]);
    return 0;
}