A – Limited Insertion
这个 \(n \leq 100\),考虑最后一次插入,然后复原出来即可。
// A.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 110;
int n, ai[MAX_N];
vector<int> seq;
int main()
{
bool valid = true;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &ai[i]), seq.push_back(ai[i]);
stack<int> st;
while (!seq.empty())
{
int pos = 0;
for (int i = 0, siz = seq.size(); i < siz; i++)
if (seq[i] == i + 1)
pos = i + 1;
if (pos == 0)
puts("-1"), exit(0);
seq.erase(seq.begin() + pos - 1);
st.push(pos);
}
while (!st.empty())
printf("%d\n", st.top()), st.pop();
return 0;
}
B – Balanced Neighbors
随手画一画,发现完全图可以做到对于每一个 \(i\) 有 \(S_i = \frac{n(n + 1)}{2} – i\),那么其实如果是偶数图,我们完全可以舍弃掉一个 \(n\),也就是不连接 \(n – i\)。如果是奇数图,我们把配对和固定为 \(n – 1\),所有的点都连接 \(n\) 即可。
// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 110;
int n;
int main()
{
scanf("%d", &n);
int b = n & 1;
n -= b;
vector<pair<int, int>> ansBox;
for (int i = 1; i <= (n << 1); i++)
{
for (int j = i + 1; j <= n; j++)
if (j != i && j != (n - i + 1))
ansBox.push_back(make_pair(i, j));
}
if (b)
{
n += b;
for (int i = 1; i < n; i++)
ansBox.push_back(make_pair(i, n));
}
printf("%lld\n", 1LL * ansBox.size());
for (auto x : ansBox)
printf("%d %d\n", x.first, x.second);
return 0;
}
C – Three Circuits
令人无语的结论题。
首先度数都要是偶数。然后考虑中枢节点,那么如果最大度数大于 \(4\),那么显然可以对边进行染色得到三个欧拉子图。如果度数为 \(4\),那么如果存在以下情况则存在划分方式,否则 GG:
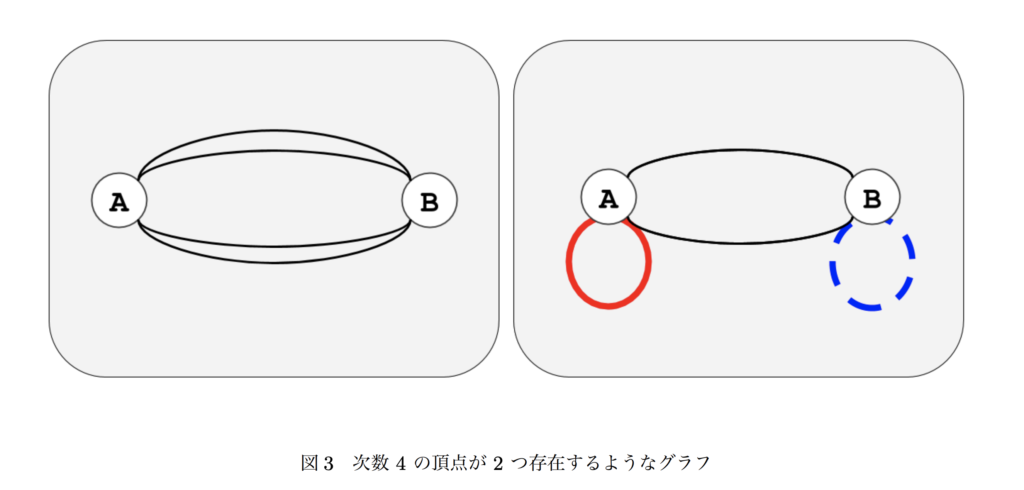
// C.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e5 + 200;
int n, m, head[MAX_N], current, deg[MAX_N], A, B;
bool vis[MAX_N];
struct edge
{
int to, nxt;
} edges[MAX_N << 1];
void addpath(int src, int dst)
{
edges[current].to = dst, edges[current].nxt = head[src];
head[src] = current++;
}
void dfs(int u, int fa)
{
vis[u] = true;
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (i != fa && edges[i].to != B)
if (!vis[edges[i].to])
dfs(edges[i].to, i ^ 1);
else
puts("Yes"), exit(0);
vis[u] = false;
}
int main()
{
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &m);
for (int i = 1, u, v; i <= m; i++)
scanf("%d%d", &u, &v), addpath(u, v), addpath(v, u), deg[u]++, deg[v]++;
int mdeg = 0;
for (int i = 1; i <= n; i++)
if (deg[i] & 1)
puts("No"), exit(0);
else
mdeg = max(mdeg, deg[i]);
if (mdeg == 4)
{
for (int i = 1; i <= n; i++)
if (deg[i] == 4)
if (A == 0)
A = i;
else if (B == 0)
B = i;
else
puts("Yes"), exit(0);
if (B)
dfs(A, 0);
puts("No"), exit(0);
}
else if (mdeg > 4)
puts("Yes"), exit(0);
else
puts("No"), exit(0);
return 0;
}
D – Rotation Sort
其实就是用 \(A\) 的代价把该元素放到右边任意区域、\(B\) 代价把该元素放到左边任意区域。做个 DP 吧。
// D.cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 5e3 + 200;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int n, A, B, pi[MAX_N], pos[MAX_N];
ll dp[MAX_N][MAX_N];
int main()
{
scanf("%d%d%d", &n, &A, &B);
for (int i = 1; i <= n; i++)
scanf("%d", &pi[i]), pos[pi[i]] = i;
memset(dp, 0x3f, sizeof(dp)), dp[0][0] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < i; j++)
if (dp[i - 1][j] != INF)
if (pos[i] > pos[j])
{
dp[i][i] = min(dp[i][i], dp[i - 1][j]);
dp[i][j] = min(dp[i][j], dp[i - 1][j] + B);
}
else
dp[i][j] = min(dp[i][j], dp[i - 1][j] + A);
}
printf("%lld\n", *min_element(dp[n], dp[n] + 1 + n));
return 0;
}
E – Modulo Pairing
先排序,然后通过扰动法获得结论:存在一个分割点,使得前半部分匹配都小于 \(M\)、后半部分匹配都大于 \(M\)。这个点可以 check,且我们尽量需要一个更靠左的节点(贪心)。
// E.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 2e5 + 200;
int n, m, ai[MAX_N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= 2 * n; i++)
scanf("%d", &ai[i]);
sort(ai + 1, ai + 1 + 2 * n);
int l = 0, r = n, res;
while (l <= r)
{
int mid = (l + r) >> 1;
bool valid = true;
for (int i = 2 * mid + 1; i <= (n << 1); i++)
if (ai[i] + ai[2 * n + 2 * mid + 1 - i] < m)
{
valid = false;
break;
}
if (valid)
r = mid - 1, res = mid;
else
l = mid + 1;
}
int pos = res << 1;
int ans = 0;
for (int i = 1; i <= pos; i++)
ans = max(ans, ai[i] + ai[pos - i + 1]);
for (int i = pos + 1; i <= (n << 1); i++)
ans = max(ans, (ai[i] + ai[(n << 1) + pos - i + 1]) % m);
printf("%lld\n", ans);
return 0;
}