初步认识树上差分
学习树上差分的前提是:
- 最近公共祖先(LCA)
- 线性差分
学习了这些之后,我们就可以开始学习树上差分了。树上差分的思想跟差分类似:都是在不得不求前缀和的情况下,将区间操作变为单点操作,降低复杂度。树上差分曾两次在 NOIp 系列比赛中出现过,所以学习树上差分很有必要(我怀疑是出题组不敢出树链剖分,但又要考察选手们对树上操作的熟悉程度,所以采用了这么个坑爹玩意)。我们先来学习一个基本的操作:点的链上区间加。
点的链上区间加
先搞一颗树:
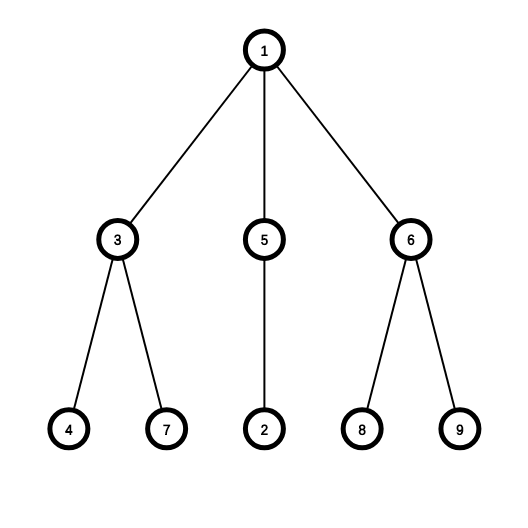
如果我们想要让链\((4,7)\)上的点标记加一,需要怎么干呢?我们可以考虑开一个数组\(tag[]\),按照差分的套路,我们可以考虑在点\(4,7\)上加一。这样的话,链\((7,3),(4,7)\)都加上了一。如果我们需要前缀和出一个答案,我们可以考虑直接在\(dfs\)回溯时计算累加。
我们会发现,起始点的 LCA 在回溯时会被计算两次,所以树上差分时,应在\(lca\)处打一个\(-1\)的标记,然后在\(lca\)的父亲处也标记一个\(-1\),来保证不受干扰。所以,整个过程非常清晰简单。
来看一道例题:
P3128 [USACO15DEC]最大流 Max Flow
FJ给他的牛棚的N(2≤N≤50,000)个隔间之间安装了N-1根管道,隔间编号从1到N。所有隔间都被管道连通了。
FJ有K(1≤K≤100,000)条运输牛奶的路线,第i条路线从隔间si运输到隔间ti。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力,你需要计算压力最大的隔间的压力是多少。
每一个隔间对应一个节点,然后对于每一条链我们都可以用树上差分打标记,最后统计答案时 \(O(n)\) 进行 DFS 就可以解出:
// P3128.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 501000;
int head[MAX_N], n, k, current, tag[MAX_N], st[20][MAX_N], tmpx, tmpy, dep[MAX_N], ans;
struct edge
{
int to, nxt;
} edges[MAX_N << 2];
void addpath(int src, int dst)
{
edges[current].to = dst, edges[current].nxt = head[src];
head[src] = current++;
}
void dfs(int u)
{
for (int i = head[u]; i != -1; i = edges[i].nxt)
{
if (edges[i].to == st[0][u])
continue;
st[0][edges[i].to] = u, dep[edges[i].to] = dep[u] + 1;
dfs(edges[i].to);
}
}
int lca(int x, int y)
{
if (dep[x] < dep[y])
swap(x, y);
for (int i = 19; i >= 0; i--)
if (dep[st[i][x]] >= dep[y])
x = st[i][x];
if (x == y)
return x;
for (int i = 19; i >= 0; i--)
if (st[i][x] != st[i][y])
x = st[i][x], y = st[i][y];
return st[0][x];
}
void getAns(int u)
{
for (int i = head[u]; i != -1; i = edges[i].nxt)
{
if (edges[i].to == st[0][u])
continue;
getAns(edges[i].to), tag[u] += tag[edges[i].to];
}
ans = max(tag[u], ans);
}
int main()
{
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &k);
for (int i = 1; i <= n - 1; i++)
scanf("%d%d", &tmpx, &tmpy), addpath(tmpx, tmpy), addpath(tmpy, tmpx);
dep[1] = 1, dfs(1);
for (int i = 1; i < 20; i++)
for (int u = 1; u <= n; u++)
st[i][u] = st[i - 1][st[i - 1][u]];
while (k--)
{
scanf("%d%d", &tmpx, &tmpy);
int LCA = lca(tmpx, tmpy);
tag[tmpx]++, tag[tmpy]++;
tag[LCA]--, tag[st[0][LCA]]--;
}
getAns(1);
printf("%d", ans);
return 0;
}
边的链上区间加
我们现在把注意力转移到边上。我们发现,其实可以用类似的方法来搞定边上的区间加。
还是那棵树:

如果我们要把链\((3,7)\)上的边的边权全部加一,我们该如何操作呢?可以考虑把边映射到点:在树中,有\(n\)个点和\(n-1\)条边,那么我们可以令每一个点对应这个点到其父亲的点的边。这样我们便可以转换为点的链上区间操作。
但是有两个点要注意:
- 显然,根节点不对应任意一条边。
- 在实际操作时,我们会发现\(lca\)对应的边并不参与链上区间统计,所以我们把原来的「\(lca\)以及\(lca\)父亲的标记」变成「在\(lca\)处标记\(-2\)」即可。
看例题:
P2680 运输计划
公元 2044 年,人类进入了宇宙纪元。
L 国有 \(n\) 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 \(n-1\) 条航道连通了 L 国的所有星球。小 P 掌管一家物流公司, 该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从 \(u_i\) 号星球沿最快的宇航路径飞行到 \(v_i\) 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 \(j\),任意飞船驶过它所花费的时间为 \(t_j\) ,并且任意两艘飞船之间不会产生任何干扰。为了鼓励科技创新, L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 \(m\) 个运输计划。在虫洞建设完成后,这 \(m\) 个运输计划会同时开始,所有飞船一起出发。当这 \(m\) 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞, 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?
这道题比上一题麻烦很多。
首先,翻译题意:清零某一条边的边权使得给定最长链最短,求出这个最短情况的数值。我们可以考虑进行二分答案,二分出这个操作后最长链的大小。之后思考\(check\)函数的写法,发现可以对于原长度大于二分值\(mid\)的链,我们可以进行树上差分标记,然后进行\(O(n)\)统计每一条边的经过次数:如果找到一条最大的长度为\(len\)边,且这条边被所有大于\(mid\)的链经过过,那么我们可以用最长的链减去\(len\)来判断是否超过\(mid\)。这道题属于边的链上区间加,注意标记的打法。
// P2680.cpp
#include <bits/stdc++.h>
#define pr pair<int, int>
using namespace std;
const int MAX_N = 3e5 + 2000;
int n, m, head[MAX_N], current, tmpx, tmpy, tmpz, tag[MAX_N];
int fa[20][MAX_N], dist[MAX_N], dep[MAX_N], sideWeight[MAX_N];
struct edge
{
int to, nxt, weight;
} edges[MAX_N << 1];
struct route
{
int src, dst, dist, lca;
} routes[MAX_N];
void addpath(int src, int dst, int weight)
{
edges[current].to = dst, edges[current].nxt = head[src];
edges[current].weight = weight, head[src] = current++;
}
void dfs(int u)
{
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (fa[0][u] != edges[i].to)
{
dep[edges[i].to] = dep[u] + 1, fa[0][edges[i].to] = u;
dist[edges[i].to] = dist[u] + edges[i].weight;
sideWeight[edges[i].to] = edges[i].weight;
dfs(edges[i].to);
}
}
int getLCA(int x, int y)
{
if (dep[x] < dep[y])
swap(x, y);
for (int i = 19; i >= 0; i--)
if (dep[fa[i][x]] >= dep[y])
x = fa[i][x];
if (x == y)
return x;
for (int i = 19; i >= 0; i--)
if (fa[i][x] != fa[i][y])
x = fa[i][x], y = fa[i][y];
return fa[0][x];
}
bool compare(route a, route b) { return a.dist > b.dist; }
void complete(int u)
{
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].to != fa[0][u])
complete(edges[i].to), tag[u] += tag[edges[i].to];
}
bool check(int attempt)
{
memset(tag, 0, sizeof(tag));
int pubSide = 0, numOfSides = 0;
for (int i = 1; i <= m; i++)
{
if (routes[i].dist <= attempt)
break;
tag[routes[i].src]++, tag[routes[i].dst]++;
tag[routes[i].lca] -= 2;
numOfSides++;
}
complete(1);
for (int i = 1; i <= n; i++)
if (tag[i] == numOfSides)
pubSide = max(pubSide, sideWeight[i]);
return routes[1].dist - pubSide <= attempt;
}
int main()
{
int l = 0, r = 0;
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &m);
for (int i = 1; i <= n - 1; i++)
{
scanf("%d%d%d", &tmpx, &tmpy, &tmpz), l = max(l, tmpz);
addpath(tmpx, tmpy, tmpz), addpath(tmpy, tmpx, tmpz);
}
dep[1] = 1, dfs(1);
for (int i = 1; i < 20; i++)
for (int j = 1; j <= n; j++)
fa[i][j] = fa[i - 1][fa[i - 1][j]];
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &tmpx, &tmpy);
route &curt = routes[i];
curt.src = tmpx, curt.dst = tmpy, curt.lca = getLCA(tmpx, tmpy);
curt.dist = dist[tmpx] + dist[tmpy] - 2 * dist[curt.lca];
r = max(r, curt.dist);
}
sort(routes + 1, routes + 1 + m, compare);
l = r - l;
while (l <= r)
if (check((l + r) >> 1))
r = ((l + r) >> 1) - 1;
else
l = ((l + r) >> 1) + 1;
printf("%d", l);
return 0;
}