A – 两情
这道题人类智慧,我真不知道咋推。
从中间开始向外扩展,然后碰到\(\gcd = 1\)的情况就输出答案即可。
// A.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n, T;
ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); }
int main()
{
scanf("%d", &T);
while (T--)
{
scanf("%lld", &n);
for (ll i = n >> 1, j = (n + 1) >> 1; i >= 1 && j <= n; i--, j++)
if (gcd(i, j) == 1)
{
printf("%lld\n", i * j / gcd(i, j));
break;
}
}
return 0;
}
B – 若是
这道题用前缀和搞暴力是真的舒适。
首先做一个前缀和,然后在枚举右下角的点,再枚举\(k\),为上矩形的行号:
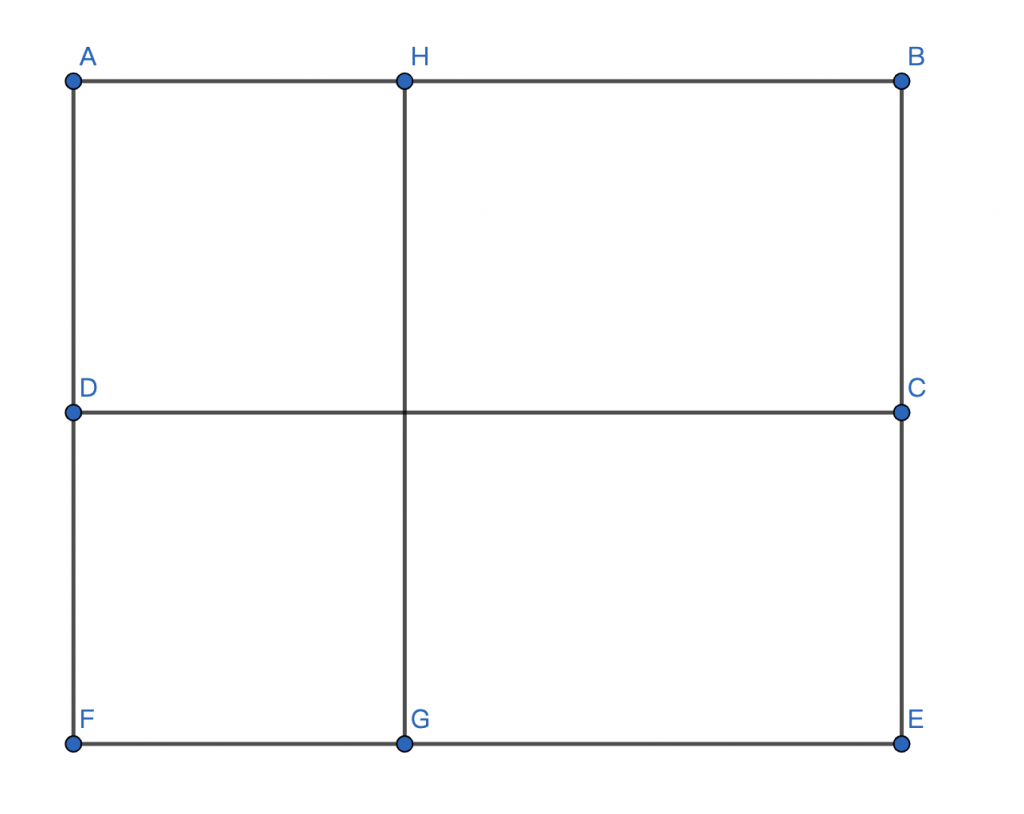
参考点\(A\)为\((0, 0)\)。然后整个子矩形的和应该是\(prefix[i][j] – prefix[i][k] – prefix[l][j] + prefix[l][k]\)。然后为了找到最大值,我们可以扫描的时候记录\(prefix[i][j] – prefix[k][j]\)的最小值即可,正好卡在\(O(n^3)\)。
// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 220;
int n, m, val[MAX_N][MAX_N], prefix[MAX_N][MAX_N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &val[i][j]), prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + val[i][j];
int mx_ans = -0x3f3f3f3f;
for (int i = 1; i <= n; i++)
for (int k = 0; k < i; k++)
for (int j = 0, min_val = 0x3f3f3f3f; j <= m; j++)
{
min_val = min(min_val, prefix[i][j] - prefix[k][j]);
mx_ans = max(mx_ans, prefix[i][j] - prefix[k][j] - min_val);
continue;
}
printf("%d", mx_ans);
return 0;
}
C – 长久时
这道题典型的 CDQ 分治,但是没想到具体怎么搞,然后 GG。
像所有 CDQ 分治一样,我们按照原序列的顺序解决子问题。每一层都要计算出左点对右问的贡献,然后继续递归即可。
三角形就直接按照正常的方法排序就行了:以他们的坐标和为关键字进行排序的时候就可以让后面的点包括在询问之中。
// C.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 3e5 + 200;
int n, answer[MAX_N], xi[MAX_N], yi[MAX_N], xtot, ytot, tot;
struct tup
{
int x, y, limit, val;
bool operator<(const tup &tgt) const { return limit < tgt.limit || (limit == tgt.limit && abs(val) < abs(tgt.val)); }
} pool[MAX_N], tmp[MAX_N];
int tree1[MAX_N], tree2[MAX_N];
inline int lowbit(int x) { return x & -x; }
int query(int *arr, int x)
{
int ans = 0;
for (; x; x -= lowbit(x))
ans += arr[x];
return ans;
}
void update(int *arr, int x, int upper, int d)
{
for (; x <= upper; x += lowbit(x))
arr[x] += d;
}
void process(int cnt)
{
sort(tmp + 1, tmp + 1 + cnt);
int pt = 0;
for (int i = 1; i <= cnt; i++)
if (tmp[i].val != 0)
{
int val = abs(tmp[i].val), opt = val / tmp[i].val;
answer[val] += opt * (pt - query(tree1, tmp[i].x) - query(tree2, tmp[i].y));
}
else
pt++, update(tree1, tmp[i].x, xtot, 1), update(tree2, tmp[i].y, ytot, 1);
for (int i = 1; i <= cnt; i++)
if (tmp[i].val == 0)
update(tree1, tmp[i].x, xtot, -1), update(tree2, tmp[i].y, ytot, -1);
}
void cdq(int l, int r)
{
int mid = (l + r) >> 1, ptr1 = 0, ptr2 = 0;
for (int i = l; i <= mid; i++)
if (pool[i].val == 0)
tmp[++ptr1] = pool[i];
for (int i = mid + 1; i <= r; i++)
if (pool[i].val != 0)
tmp[ptr1 + (++ptr2)] = pool[i];
if (ptr1 > 0 && ptr2 > 0)
process(ptr1 + ptr2);
if (ptr1 > 0 && ptr1 <= mid - l)
cdq(l, mid);
if (ptr2 > 0 && ptr2 < r - mid)
cdq(mid + 1, r);
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
int x, y, d;
scanf("%d%d%d", &x, &y, &d);
if (d == 0)
xi[++xtot] = x, yi[++ytot] = y, pool[++tot] = {x, y, x + y, 0}, answer[i] = -1;
else
{
xi[++xtot] = x - 1, yi[++ytot] = y - 1;
pool[++tot] = {x - 1, y - 1, x + y - 1, -i};
pool[++tot] = {x - 1, y - 1, x + y + d, i};
}
}
sort(xi + 1, xi + 1 + xtot), xtot = unique(xi + 1, xi + 1 + xtot) - xi - 1;
sort(yi + 1, yi + 1 + ytot), ytot = unique(yi + 1, yi + 1 + ytot) - yi - 1;
for (int i = 1; i <= tot; i++)
{
pool[i].x = lower_bound(xi + 1, xi + 1 + xtot, pool[i].x) - xi;
pool[i].y = lower_bound(yi + 1, yi + 1 + ytot, pool[i].y) - yi;
}
cdq(1, tot);
for (int i = 1; i <= n; i++)
if (answer[i] >= 0)
printf("%d\n", answer[i]);
return 0;
}