Kalorona

「Fortuna OJ」Mar 7th – Group A 解题报告

A – 高维宇宙

裸的二分图匹配，匹配数除以二即可。

// A.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 100;
int head[MAX_N], n, current, matching[MAX_N], dfn[MAX_N], arr[MAX_N];
bool isPrime[2020];
struct edge
{
    int to, nxt;
} edges[(MAX_N * (MAX_N - 1)) >> 1];
void addpath(int src, int dst)
{
    edges[current].to = dst, edges[current].nxt = head[src];
    head[src] = current++;
}
bool dfs(int u, int org)
{
    for (int i = head[u]; i != -1; i = edges[i].nxt)
    {
        int to = edges[i].to;
        if (dfn[to] != org)
        {
            dfn[to] = org;
            if ((!matching[to]) || dfs(matching[to], org))
            {
                matching[to] = u;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    freopen("prime.in", "r", stdin);
    freopen("prime.out", "w", stdout);
    memset(head, -1, sizeof(head)), memset(isPrime, true, sizeof(isPrime));
    int ans = 0;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &arr[i]);
    for (int i = 2; i < 2020; i++)
        if (isPrime[i])
            for (int j = 2; i * j < 2020; j++)
                isPrime[j * i] = false;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (isPrime[arr[i] + arr[j]])
                addpath(i, j);
    for (int i = 1; i <= n; i++)
        if (dfs(i, i))
            ans++;
    printf("%d", ans / 2);
    return 0;
}

B – 排队

这道题我在考场上 A 掉了，方法跟题解不太一样（欢迎来 Hack），当然复杂度可能会高一点。

我们考虑魔改 DFS 序，在进入节点之前先进行排序，排序之后 DFS 完了之后再进行标记。可以发现，这就是我们在不删除节点的情况下的最优放法：

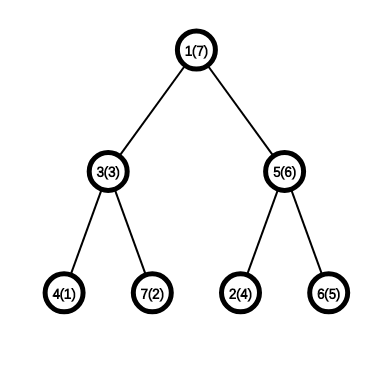
如上图所示，这就是我们在不搞删除的情况下放置的最佳顺序：4、7、3、2、6、5、1。我们定义这种顺序叫做乱搞序。我们来讨论使用一种乱搞的线段树（以上面那种顺序做关键字）来搞定这两个操作。

\(OPT = 1\)的情况下：我们先考虑之前没有删除操作的情况，其实很简单，直接往最后一个乱搞序最小的槽位设置为一即可；如果之前有过删除操作的话，那么已有的乱搞序上肯定不是连续的1：一定有个0表示被删除，我们可以考虑在 UPDATE 操作里面判断左右儿子是否有不满足连续的情况（也就是和等于区间长度），如果有那么就从加数里取出一些，如果加数有剩余，那么左儿子直接打标记，然后递归右儿子：因为我们设置 UPDATE 操作的返回值为最后一个乱搞值，之后通过 anti 数组重新转换为节点编号。

int update(int l, int r, int p, int c)
{
    if (c == 0)
        return -1;
    if (l == r)
    {
        tree[p] += c;
        return l;
    }
    int lft = (mid - l + 1) - tree[lson], rig = c - lft;
    int ans = 0;
    if (rig > 0)
    {
        tree[lson] = mid - l + 1, lazy[lson] = 1;
        ans = update(mid + 1, r, rson, rig);
    }
    else
        ans = update(l, mid, lson, c);
    tree[p] = tree[lson] + tree[rson];
    return ans;
}

\(OPT=2\)的情况下也比较简单，我们只要找出该节点到根节点链上的已用节点个数并减去一即可，进行单点修改。

建议详读代码，理解我的乱搞思想。

// B.cpp
#include <bits/stdc++.h>
#define mid ((l + r) >> 1)
#define lson (p << 1)
#define rson ((p << 1) | 1)
#define lowbit(x) (x & -x)
using namespace std;
const int MAX_N = 1e5 + 2000;
int n, t, dfn[MAX_N], st[20][MAX_N], tmpx, tmpy, tree[MAX_N << 2], lazy[MAX_N << 2], dtot, anti[MAX_N];
vector<int> G[MAX_N];
void addpath(int src, int dst) { G[src].push_back(dst); }
void pushdown(int p, int l, int r)
{
    if (lazy[p] && l != r)
    {
        tree[lson] = mid - l + 1, tree[rson] = r - mid;
        lazy[lson] = 1, lazy[rson] = 1;
    }
    lazy[p] = 0;
}
int update(int l, int r, int p, int c)
{
    if (c == 0)
        return -1;
    if (l == r)
    {
        tree[p] += c;
        return l;
    }
    int lft = (mid - l + 1) - tree[lson], rig = c - lft;
    int ans = 0;
    if (rig > 0)
    {
        tree[lson] = mid - l + 1, lazy[lson] = 1;
        ans = update(mid + 1, r, rson, rig);
    }
    else
        ans = update(l, mid, lson, c);
    tree[p] = tree[lson] + tree[rson];
    return ans;
}
void remove(int qx, int l, int r, int p)
{
    if (l == r && l == qx)
    {
        tree[p] = 0, lazy[p] = 0;
        return;
    }
    pushdown(p, l, r);
    if (qx <= mid)
        remove(qx, l, mid, lson);
    else
        remove(qx, mid + 1, r, rson);
    tree[p] = tree[lson] + tree[rson];
}
bool query(int qx, int l, int r, int p)
{
    if (l == r && l == qx)
        return tree[p];
    pushdown(p, l, r);
    if (qx <= mid)
        return query(qx, l, mid, lson);
    else
        return query(qx, mid + 1, r, rson);
}
void dfs(int u)
{
    sort(G[u].begin(), G[u].end());
    int siz = G[u].size();
    for (int i = 0; i < siz; i++)
    {
        int to = G[u][i];
        if (st[0][u] != to)
            st[0][to] = u, dfs(to);
    }
    dfn[u] = ++dtot, anti[dfn[u]] = u;
}
int main()
{
    scanf("%d%d", &n, &t);
    for (int i = 1; i <= n - 1; i++)
        scanf("%d%d", &tmpx, &tmpy), addpath(tmpx, tmpy), addpath(tmpy, tmpx);
    dfs(1);
    for (int i = 1; i < 20; i++)
        for (int j = 1; j <= n; j++)
            st[i][j] = st[i - 1][st[i - 1][j]];
    while (t--)
    {
        int opt, x;
        scanf("%d%d", &opt, &x);
        if (opt == 1)
            printf("%d\n", anti[update(1, n, 1, x)]);
        else
        {
            int u = x, ans = 0;
            for (int i = 19; i >= 0; i--)
                if (st[i][u] != 0 && query(dfn[st[i][u]], 1, n, 1) == true)
                    u = st[i][u], ans += 1 << i;
            printf("%d\n", ans);
            remove(dfn[u], 1, n, 1);
        }
    }
    return 0;
}

C – 心理学概论

我考场上以为是费用流，然后打凉掉了。

可以考虑先对序列进行排序（按第一、二和三关键字），然后再进行分段：二分出两个位置\(mid,mid1\)，然后分成三段：\( [1,mid],[mid+1,mid1],[mid1+1,n] \)

之后统计即可。

// C.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 1e5 + 1000;
struct cas
{
    ll x, y, z;
    bool operator<(const cas &cs) const { return x < cs.x || (cs.x == x && y < cs.y) || (y == cs.y && x == cs.x && z < cs.z); }
} cases[MAX_N];
ll n, ans1, ans2, ans3, ans;
int main()
{
    freopen("psy.in", "r", stdin);
    freopen("psy.out", "w", stdout);
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%lld%lld%lld", &cases[i].x, &cases[i].y, &cases[i].z);
        ans1 = max(ans1, cases[i].x), ans2 = max(ans2, cases[i].y), ans3 = max(ans3, cases[i].z);
    }
    ans = min(ans1, min(ans2, ans3));
    sort(cases + 1, cases + 1 + n);
    ll l = 0, r = n, l1 = 0, r1 = n;
    while (l < r)
    {
        ll mid = (l + r) >> 1;
        l1 = 0, r1 = n;
        bool flag = true;
        while (l1 < r1)
        {
            ll mid1 = (l1 + r1) >> 1;
            if (mid1 == mid)
                if (mid1 + 1 <= r)
                    mid1++;
                else if (mid1 - 1 >= l)
                    mid1--;
                else
                {
                    flag = false;
                    break;
                }
            ll k = 0;
            for (int i = 1; i <= n; i++)
            {
                if (cases[i].x <= cases[mid].x)
                    continue;
                if (cases[i].y <= cases[mid1].y)
                    continue;
                if (cases[i].z > k)
                    k = cases[i].z;
            }
            ans1 = cases[mid].x + cases[mid1].y + k;
            if (ans1 < ans)
                ans = ans1, flag = true, r1 = mid1;
            else
                l1 = mid1 + 1;
        }
        if (flag)
            r = mid;
        else
            l = mid + 1;
    }
    ll k = 0;
    for (int i = 1; i <= n; i++)
    {
        if (cases[i].x <= cases[l].x)
            continue;
        if (cases[i].y <= cases[l1].y)
            continue;
        if (cases[i].z > k)
            k = cases[i].z;
    }
    ans = min(ans, cases[l].x + cases[l1].y + k);
    printf("%lld", ans);
    return 0;
}

P3924:康娜的线段树题解

思路

这道题很好，很有趣。

如果您是神仙的话呢，可以考虑直接线段是卡掉本题（有人试过了），但是我这个菜鸡不行，所以写了题解的\(O(1)\)询问解法。

首先，树形 DP 的方程为：

\[ dp[u] = \frac{1}{2} * (dp[lson]+dp[rson]) \]

我们观察叶子节点对答案的贡献，发现为该条链上的权值和除掉\(2^{dep-1}\)，也就是与深度有关。那么，为了简化答案，我们可以把这个写作：

\[ \frac{1}{2^{dep-1}} = 2^{1-dep} = \frac { 2^{maxDep – dep} }{ 2^{maxDep-1} } \]

就变成了乘法形式。我们在讨论询问的问题。在区间\([l,r]\)之间加上\(x\)，链对答案的贡献是：

\[ x · \sum_{i = 1}^{dep} \frac{1}{2^{i-1}} \]

所以，维护一个前缀和，往答案上面加上前缀和段和这个贡献的积即可获得答案。（记得用 gcd 约分）

代码

// P3924.cpp
#include <bits/stdc++.h>
#define ll long long
#define mid ((l + r) >> 1)
#define lson (p << 1)
#define rson ((p << 1) | 1)
using namespace std;
const int MAX_N = 1e6 + 2000;
ll n, m, qwq, sum[MAX_N << 2], depth[MAX_N << 2], arr[MAX_N], s[MAX_N], max_dep;
inline ll read()
{
    ll s = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
        s = s * 10 + ch - '0', ch = getchar();
    return s * w;
}
void build(ll l, ll r, ll dp, ll p)
{
    if (l == r)
    {
        sum[p] = arr[l], depth[l] = dp, max_dep = max(max_dep, dp);
        return;
    }
    build(l, mid, dp + 1, lson), build(mid + 1, r, dp + 1, rson);
    sum[p] = sum[lson] + sum[rson];
}
ll query(ll l, ll r, ll p, ll dep, ll prefix)
{
    if (l == r)
        return (1 << dep) * (prefix + sum[p]);
    return query(l, mid, lson, dep - 1, prefix + sum[p]) + query(mid + 1, r, rson, dep - 1, prefix + sum[p]);
}
ll gcd(ll a, ll b) { return (b == 0) ? a : gcd(b, a % b); }
int main()
{
    n = read(), m = read(), qwq = read();
    for (int i = 1; i <= n; i++)
        arr[i] = read();
    build(1, n, 1, 1);
    ll ans = query(1, n, 1, max_dep - 1, 0), dominator = 1 << (max_dep - 1);
    ll fact = gcd(dominator, qwq);
    dominator /= fact, qwq /= fact;
    for (int i = 1; i <= n; i++)
        s[i] = s[i - 1] + (((1 << depth[i]) - 1) << (max_dep - depth[i]));
    while (m--)
    {
        ll l = read(), r = read(), w = read();
        ans += (s[r] - s[l - 1]) * w;
        printf("%lld\n", ans / dominator * qwq);
    }
    return 0;
}

Codeforces 1106F:Lunar New Year and a Recursive Sequence 题解

主要思路

哇这道题还是很神仙的。

首先，有递推式：

\[ f_i = \left(\prod_{j = 1}^{k} f_{i – j}^{b_j}\right) \bmod p \]

题目会给出一个\(f_n=m\)，且这个数列前面的项都是\(1\)，可看作次数为\(0\)的常数项。我们会发现，对于\(f_j,j>k\)，都可以写成\(f_k^{C}\)，其中\(C\)是一个多项式。这个多项式可以通过线性递推得到：

\[ C_i = (\sum_{j = 1}^{k} b_jC_{i-j}) \mod (p-1) \]

看到数据范围，考虑用矩阵乘法在\(O(n^3 \log n)\)的时间内得到\(C_n\)。所以现在我们有：

\[ f_k^{C_k} \equiv m \;(mod \; p) \]

我们现在已知\(k,m,p,C_n\)，我们现在要求\(f_k\)。考虑使用原根来搞。众所周知，998244353 的原根是 3。原根的幂可以填充整个模\(p\)剩余系，所以可以考虑把这个式子写成：

\[ (3^t)^{C_k} \equiv 3^s \;(mod \; p), \text{其中设}m = 3^s, f_k = 3^t \]

我们把离散对数搞下来，变成：

\[ t*C_k \equiv s \; (mod \; p-1) \]

这个用 BSGS 搞下就可以得出结果\(s\)。然后用 exgcd 算出同余方程的解（顺便判别有无解）。算出\(t\)之后快速幂一下输出。

代码

// CF1106F.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
// TODO: Make it fit to the matrix power;
const int MAX_MAT = 150, mod = 998244353;
int n, m, k, ki[MAX_MAT];
struct matrix
{
    ll mat[MAX_MAT][MAX_MAT];
    void basify()
    {
        for (int i = 1; i <= k; i++)
            mat[i][i] = 1;
    }
    ll *operator[](const int &id) { return mat[id]; }
    matrix operator*(const matrix &mt) const
    {
        matrix ans;
        memset(ans.mat, 0, sizeof(ans.mat));
        for (int i = 1; i <= k; i++)
            for (int j = 1; j <= k; j++)
                for (int mid = 1; mid <= k; mid++)
                    ans.mat[i][j] = (ans.mat[i][j] + mat[i][mid] * mt.mat[mid][j] % (mod - 1)) % (mod - 1);
        return ans;
    }
    matrix operator^(const int &tim) const
    {
        matrix ans, bas = *this;
        ans.basify();
        int ti = tim;
        while (ti)
        {
            if (ti & 1)
                ans = ans * bas;
            bas = bas * bas;
            ti >>= 1;
        }
        return ans;
    }
};
ll quick_pow(ll bas, ll tim)
{
    ll ans = 1;
    while (tim)
    {
        if (tim & 1)
            ans = ans * bas % mod;
        bas = bas * bas % mod;
        tim >>= 1;
    }
    return ans;
}
ll bsgs(ll a, ll y)
{
    if (a == 0 && y == 0)
        return 1;
    if (a == 0 && y != 0)
        return -1;
    map<ll, ll> hsh;
    ll u = ceil(sqrt(mod));
    for (int i = 0, x = 1; i <= u; i++, x = x * a % mod)
        hsh[y * x % mod] = i;
    ll unit = quick_pow(a, u);
    for (int i = 1, x = unit; i <= u; i++, x = x * unit % mod)
        if (hsh.count(x))
            return i * u - hsh[x];
    return -1;
}
ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y), z = x;
    x = y, y = z - (a / b) * y;
    return d;
}
ll gcd(ll a, ll b) { return (b == 0) ? a : gcd(b, a % b); }
ll solve(ll a, ll b, ll c)
{
    if (b == 0)
        return 0;
    ll d = gcd(a, b);
    a /= d, b /= d;
    if (gcd(a, c) != 1)
        return -1;
    ll res, tmp;
    exgcd(a, c, res, tmp);
    res = res * b % c;
    res = (res + c) % c;
    return res;
}
int main()
{
    scanf("%d", &k);
    for (int i = 1; i <= k; i++)
        scanf("%d", &ki[i]);
    scanf("%d%d", &n, &m);
    matrix B;
    for (int i = 1; i <= k; i++)
        B[1][i] = ki[i];
    for (int i = 2; i <= k; i++)
        B[i][i - 1] = 1;
    B = B ^ (n - k);
    ll res = B[1][1], s = bsgs(3, m), ans = solve(res, s, mod - 1);
    if (ans == -1)
        puts("-1");
    else
        printf("%lld", quick_pow(3, ans));
    return 0;
}

「Fortuna OJ」Mar 5th – Group A 解题报告

A – 旷野大计算

嗯，是我这种菜鸡不会的类型。

这个题主要的思路就是用离线莫队算法，这个算法是我本人第一次打，所以我会尝试一处一处讲清楚。首先大致分析一下，这道题的本质其实就是查询区间最大的加权众数。那么，根据题解上讲的，有一个这样的结论：

给定集合\(A,B\)，则\(mode(A \cup B) \to mode(A) \cup B\)这两玩意本质一样。

所以就可以考虑进行区间增大的莫队了。首先，离散化后简单的分个块，把问答离线下来排个序搞一搞。针对每一个询问，如果可以从上个区间进行转移，就进行快速转移；否则，重新开始。

莫队算法的精髓就是：暴力的进行转移。

// A.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 1e6 + 2000;
int n, m, arr[MAX_N], blockId[MAX_N];
int currentId[MAX_N], bucket[MAX_N];
ll cnt[MAX_N], leftBucket[MAX_N], answer, anses[MAX_N];
struct query
{
    int l, r, id;
    bool operator<(const query &qu) const
    {
        return blockId[l] < blockId[qu.l] ||
               (blockId[l] == blockId[qu.l] && r < qu.r);
    }
} queries[MAX_N];
void update_left(int x)
{
    leftBucket[currentId[x]]++;
    answer = max(answer, (leftBucket[currentId[x]] + cnt[currentId[x]]) * 1LL * arr[x]);
}
int main()
{
    scanf("%d%d", &n, &m);
    int siz = sqrt(n * 1.0);
    for (int i = 1; i <= n; i++)
        scanf("%d", &arr[i]), bucket[i] = arr[i], blockId[i] = (i - 1) / siz + 1;
    sort(bucket + 1, bucket + 1 + n);
    int buckTot = unique(bucket + 1, bucket + 1 + n) - bucket;
    for (int i = 1; i <= n; i++)
        currentId[i] = lower_bound(bucket + 1, bucket + 1 + buckTot, arr[i]) - bucket;
    for (int i = 1; i <= m; i++)
        scanf("%d%d", &queries[i].l, &queries[i].r), queries[i].id = i;
    sort(queries + 1, queries + 1 + m);
    // Previous Information:
    int L = 1, R = 0, tmd;
    ll tmp = 0;
    answer = 0;
    queries[0].l = 0, blockId[0] = 0;
    for (int i = 1; i <= m; i++)
    {
        // Validiate if this interval is able to be calced by the previous one;
        if (blockId[queries[i - 1].l] != blockId[queries[i].l])
        {
            memset(cnt, 0, sizeof(cnt));
            R = tmd = blockId[queries[i].l] * siz;
            answer = tmp = 0;
        }
        L = min(tmd + 1, queries[i].r + 1);
        // Calc;
        while (L > queries[i].l)
            update_left(--L);
        while (R < queries[i].r)
        {
            R++;
            tmp = max((++cnt[currentId[R]]) * 1LL * arr[R], tmp);
            answer = max(answer, (cnt[currentId[R]] + leftBucket[currentId[R]]) * 1LL * arr[R]);
        }
        // Set the answer;
        anses[queries[i].id] = answer;
        // Set the bucket back;
        for (int j = L; j <= queries[i].r && j <= tmd; j++)
            leftBucket[currentId[j]]--;
        answer = tmp;
    }
    // Print the answer;
    for (int i = 1; i <= m; i++)
        printf("%lld\n", anses[i]);
    return 0;
}

B – 爬山

这是一道傻逼题，然后我强行搞了个拓扑序 DP 就 GG 了。现在想想非常后悔。

显然，把环全部缩成点就会形成一个 DAG （有向无环图），之后直接暴力 DP，然后再取出标记过的答案进行最大值比较即可。很傻逼的一道题。

哦，对了，记得开栈。（JZOJ 万年卡栈）

// B.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 602000;
extern int theMain(void) __asm__("theMain");
int head[MAX_N << 1], current, n, m, dfn[MAX_N], low[MAX_N], aff[MAX_N];
int tot, stk[MAX_N], cur, afftot, indeg[MAX_N << 1], tmpx, tmpy, s;
ll cnt[MAX_N << 1], dp[MAX_N << 1], answer;
bool inst[MAX_N], mark[MAX_N];
struct edge
{
    int to, nxt;
} edges[MAX_N << 1];
void addpath(int src, int dst)
{
    edges[current].to = dst;
    edges[current].nxt = head[src], head[src] = current++;
}
void tarjan(int u)
{
    dfn[u] = low[u] = ++tot, stk[++cur] = u, inst[u] = true;
    for (int i = head[u]; i != -1; i = edges[i].nxt)
        if (dfn[edges[i].to] == 0)
            tarjan(edges[i].to), low[u] = min(low[u], low[edges[i].to]);
        else if (inst[edges[i].to])
            low[u] = min(low[u], dfn[edges[i].to]);
    if (low[u] == dfn[u])
    {
        int j, nd = ++afftot;
        do
        {
            j = stk[cur], inst[j] = false;
            aff[j] = nd;
        } while (stk[cur--] != u);
    }
}
void toposort()
{
    queue<int> q;
    q.push(aff[s]), dp[aff[s]] = cnt[aff[s]];
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        for (int i = head[u]; i != -1; i = edges[i].nxt)
        {
            dp[edges[i].to] = max(dp[edges[i].to], dp[u] + cnt[edges[i].to]);
            q.push(edges[i].to);
        }
    }
}
int theMain()
{
    memset(head, -1, sizeof(head));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
        scanf("%d%d", &tmpx, &tmpy), addpath(tmpx, tmpy);
    afftot = n;
    for (int i = 1; i <= n; i++)
        if (aff[i] == 0)
            tarjan(i);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &cnt[i]);
    for (int u = 1; u <= n; u++)
    {
        cnt[aff[u]] += cnt[u];
        for (int i = head[u]; i != -1; i = edges[i].nxt)
            if (aff[u] != aff[edges[i].to])
                addpath(aff[u], aff[edges[i].to]), indeg[aff[edges[i].to]]++;
    }
    scanf("%d%d", &s, &tmpx);
    for (int i = 1; i <= tmpx; i++)
        scanf("%d", &tmpy), mark[aff[tmpy]] = true;
    toposort();
    for (int i = 1; i <= n; i++)
        if (mark[aff[i]])
            answer = max(answer, dp[aff[i]]);
    printf("%lld", answer);
    return 0;
}

int main()
{
    int size = 64 << 20;
    char *p = (char *)malloc(size) + size;
    __asm__ __volatile__("movq  %0, %%rsp\n"
                         "pushq $exit\n"
                         "jmp theMain\n" ::"r"(p));
    return 0;
}

C – 货仓选址 运输妹子

如题，然后秒切。

// C.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 101000;
ll n, l, w, pos[MAX_N], prefix[MAX_N], answer;
bool validiate(int l, int r)
{
    int mid = (l + r) >> 1;
    ll ans = pos[mid] * (mid - l + 1) - (prefix[mid] - prefix[l - 1]) + (prefix[r] - prefix[mid]) - pos[mid] * (r - mid);
    return ans <= w;
}
int main()
{
    scanf("%lld%lld%lld", &n, &l, &w);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &pos[i]), prefix[i] = prefix[i - 1] + pos[i];
    ll lcur = 1, rcur = 0;
    while (rcur < n && lcur <= n)
    {
        rcur++;
        while (lcur <= rcur && !validiate(lcur, rcur))
            lcur++;
        answer = max(rcur - lcur + 1, answer);
    }
    printf("%lld", answer);
    return 0;
}

「Fortuna OJ」Mar 4th – Group A 解题报告

A – 漆黑列车载运数个谎言

这道题应该是并查集域的裸题，不讲。

// A.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e6 + 200;
int n, m, fa[MAX_N << 2];
int find(int x) { return fa[x] == x ? fa[x] : fa[x] = find(fa[x]); }
void unite(int x, int y) { fa[find(x)] = fa[find(y)]; }
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= 2 * n; i++)
        fa[i] = i;
    while (m--)
    {
        int opt, x, y;
        scanf("%d%d%d", &opt, &x, &y);
        if (opt == 0)
            unite(x, y), unite(x + n, y + n);
        else if (opt == 1 || opt == 2)
            unite(x, y + n), unite(x + n, y);
        else if (find(x) == find(y) || find(x + n) == find(y + n))
            puts("1");
        else
            puts("0");
    }
    return 0;
}

Continue reading →

「Fortuna OJ」Mar 2nd – Group A 解题报告

今天比赛状态极差，又困、又饿，眼睛又干。

A – 拯救奶牛

我们先把问题转换为三角矩阵上两点的距离，可以类比曼哈顿距离，我们可以把距离分为纵向和横向两种来考虑。

首先是纵向。如果\((x_1,y_1)\)要到\((x_2,y_2)\)，那么分下面几种情况：

  • 如果\(x_1\)和\(x_2\)的奇偶性不同，那么贡献为\(2|x_1-x_2|-1\)。
  • 如果相同，那么贡献为\(2|x_1-x_2|\)。

那么再来看横向。我们发现，如果我们把上方的三角形扩大成这样：

我们发现，这一范围内的三角形不需要额外的横向贡献，只需要计算纵向贡献即为答案。对于在同一行却不在这个区域内的三角形，横向贡献也非常好计算，做差乘二即可。

记得要对输入点进行排序。

代码

// A.cpp
#include <bits/stdc++.h>
#define pr pair<int, int>
using namespace std;
const int MAX_N = 1001000;
pr prs[MAX_N];
int n, m, si, sj;
int answer, exitI, exitJ;
int main()
{
    answer = 0x3f3f3f3f;
    scanf("%d%d%d%d", &m, &n, &si, &sj);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &prs[i].first, &prs[i].second);
    sort(prs + 1, prs + 1 + n);
    for (int i = 1; i <= n; i++)
    {
        pr pta = prs[i], ptb = make_pair(si, sj);
        if (pta.first < ptb.first)
            swap(pta, ptb);
        int jl = ptb.second, jr = ptb.second + (pta.first - ptb.first) * 2;
        int ans = (pta.first - ptb.first) << 1;
        if (pta.second >= jl && pta.second <= jr &&
            (ans < answer || (ans == answer && exitJ >= prs[i].second)))
        {
            answer = ans, exitI = prs[i].first, exitJ = prs[i].second;
            if ((pta.second & 1) != (ptb.second & 1))
                answer -= 1;
            continue;
        }
        ans += min(abs(pta.second - jl), abs(pta.second - jr));
        if (ans < answer || (ans == answer && exitJ >= prs[i].second))
            answer = ans, exitI = prs[i].first, exitJ = prs[i].second;
    }
    printf("%d %d\n%d", exitI, exitJ, answer + 1);
    return 0;
}

B – 邮递员

首先，这道题的\(w_i\)毫无卵用。我们来看这个\(w_i\)对亏损的贡献：

\[ \sum_{i=1}^{n}( i-w_{s_i} )= \frac{n(n-1)}{2}-\sum_{i=1}^{n} w_i \]

所以顺序根本不会造成影响。所以，我们来找一条最短的一笔画路径且字典序最小，方可保证答案最简。

因为题目里明显的说了（可惜我没看到，眼瞎了）

能够离开每个村子的路口的数目一定是2，4或者8。

我可真是个傻逼。

所以，用邻接表存图，然后按标号从小到大进行 DFS 写栈，最后反向弹栈输出即可。

代码

// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 220;
int n, m, wi[MAX_N], tmpx, tmpy, dist[MAX_N][MAX_N], tot;
stack<int> stk;
void dfs(int u)
{
    for (int i = 1; i <= n; i++)
        if (dist[u][i])
        {
            dist[u][i]--, dist[i][u]--;
            dfs(i);
        }
    stk.push(u);
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &wi[i]);
    for (int i = 1; i <= m; i++)
        scanf("%d%d", &tmpx, &tmpy), dist[tmpx][tmpy]++, dist[tmpy][tmpx]++;
    dfs(1);
    printf("%d\n", stk.size() - 1);
    while (!stk.empty())
        printf("%d ", stk.top()), stk.pop();
    return 0;
}

C – 最小密度路径

我们可以考虑设置状态\(f[i][j][k]\)为从节点\(i\)到\(j\)走了\(k\)条边的总长度，然后 Floyd 预处理，最后\(O(n)\)回答即可，傻逼题。

代码

// C.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 55, MAX_M = 1200;
int n, m, tmpx, tmpy, tmpz, f[MAX_N][MAX_N][MAX_M], dist[MAX_N][MAX_N], q;
int main()
{
    scanf("%d%d", &n, &m);
    memset(f, 0x3f, sizeof(f)), memset(dist, 0x3f, sizeof(dist));
    for (int i = 1; i <= m; i++)
        scanf("%d%d%d", &tmpx, &tmpy, &tmpz), dist[tmpx][tmpy] = min(dist[tmpx][tmpy], tmpz);
    for (int i = 1; i <= n; i++)
        f[i][i][0] = 0;
    for (int s = 1; s <= n; s++)
        for (int k = 1; k <= n; k++)
            for (int i = 1; i <= n; i++)
                for (int j = 1; j <= n; j++)
                    if (f[i][j][s] > f[i][k][s - 1] + dist[k][j])
                        f[i][j][s] = f[i][k][s - 1] + dist[k][j];
    scanf("%d", &q);
    while (q--)
    {
        double ans = (double)0x3f3f3f3f;
        int i, j;
        bool flag = true;
        scanf("%d%d", &i, &j);
        for (int s = 1; s <= n; s++)
            if (1.0 * f[i][j][s] / (1.0 * s) < ans && f[i][j][s] != (double)0x3f3f3f3f)
                ans = min(ans, 1.0 * f[i][j][s] / (1.0 * s)), flag = false;
        if (flag)
            puts("OMG!");
        else
            printf("%.3lf\n", ans);
    }
    return 0;
}