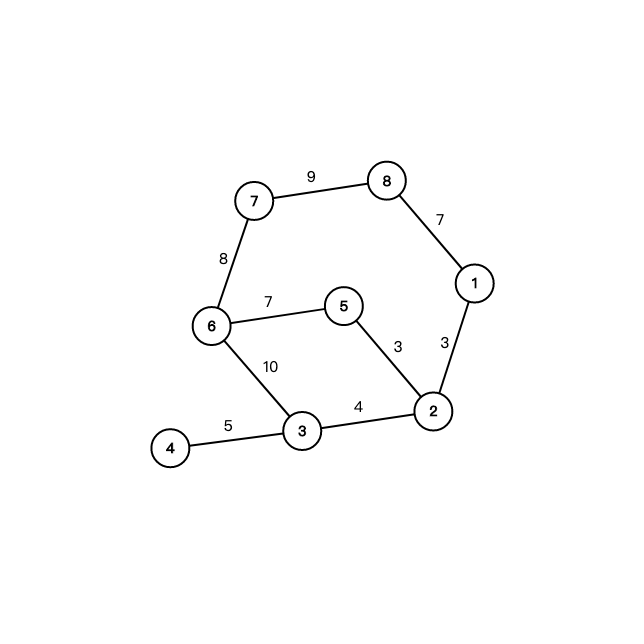
A – 铁轨
sb 题,不讲。(为什么 B 组会有这么水的题?)
B – 独立集
这道题翻译过来就是独立集计数,也是一道 sb 题。
首先,这种计数题肯定都是基于树形 DP 的,所以我们来设状态。起初,我设的状态是:该节点所在的子树的独立集个数为 \(dp[u]\)。后面发现不太对劲:状态转移时,大体可以分为两种进行计数,一种是儿子子树内的乘积(包括空集在内,这样就可以算所有的并集个数),还有一种是孙子子树和本节点的独立集。所以,这些信息要分开储存:设\(dp[u][1]\)为独立集个数,\(dp[u][0]\)孙子节点的独立集个数。所以,可以得到下列方程: