简述
一般赛场上遇上计算几何的题一般都不难,而碰上了没学过就直接爆零。为了避免这样的情况,我决定好好学一遍计算几何的一些东西。
结果是学了一遍照样爆零。
向量全家桶
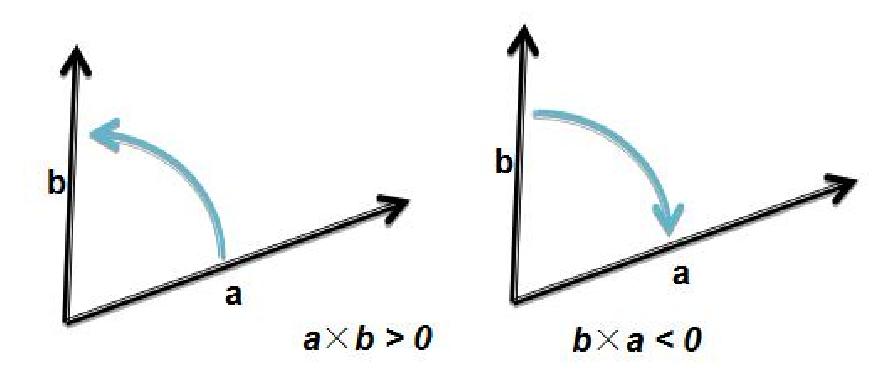
向量正常的东西没什么好说的,就单独说一下叉积的含义就可以了。叉积就是两个向量所围成的平行四边形的有向面积。具体看图可以理解:
struct vec
{
double x, y;
vec(double _x = 0, double _y = 0) : x(_x), y(_y) {}
vec operator+(const vec &rhs) { return vec(x + rhs.x, y + rhs.y); }
vec operator-(const vec &rhs) { return vec(x - rhs.x, y - rhs.y); }
double operator*(const vec &rhs) const { return x * rhs.x + y * rhs.y; }
vec operator*(const double &rhs) { return vec(x * rhs, y * rhs); }
double operator^(const vec &rhs) const { return x * rhs.y - y * rhs.x; }
vec operator/(const double &rhs) const { return vec(x / rhs, y / rhs); }
double len2() { return x * x + y * y; }
double len() { return sqrt(len2()); }
vec normalize() { return (*this) / len(); }
};
点、线
判断点与直线位置
如果现在要判断点 \(P\) 在方向向量为 \(v\) 的左右边,我们可以找一个直线上的点 \(Q\),然后判断 \(\vec{QP} \times v\) 的正负性就好了。
判断线段的相交性
首先判断线段平行的问题,这个可以判断两次叉积就可以做了。如果是重叠,就看一下有没有三点共线的情况(也可以用叉积来判角度)。解决这个东西之后,就来正式的判断是否相交。
首先判断两条线段的所占的四边形区域是否有交。如果有交就进一步的进行判断:可以试着用上面的点与直线位置来判断是否一个线段的两个端点是否在另一个线段的两侧。两者结合就可以做完了。这个东西叫做快速排斥实验和跨立实验。
求两个直线的交点
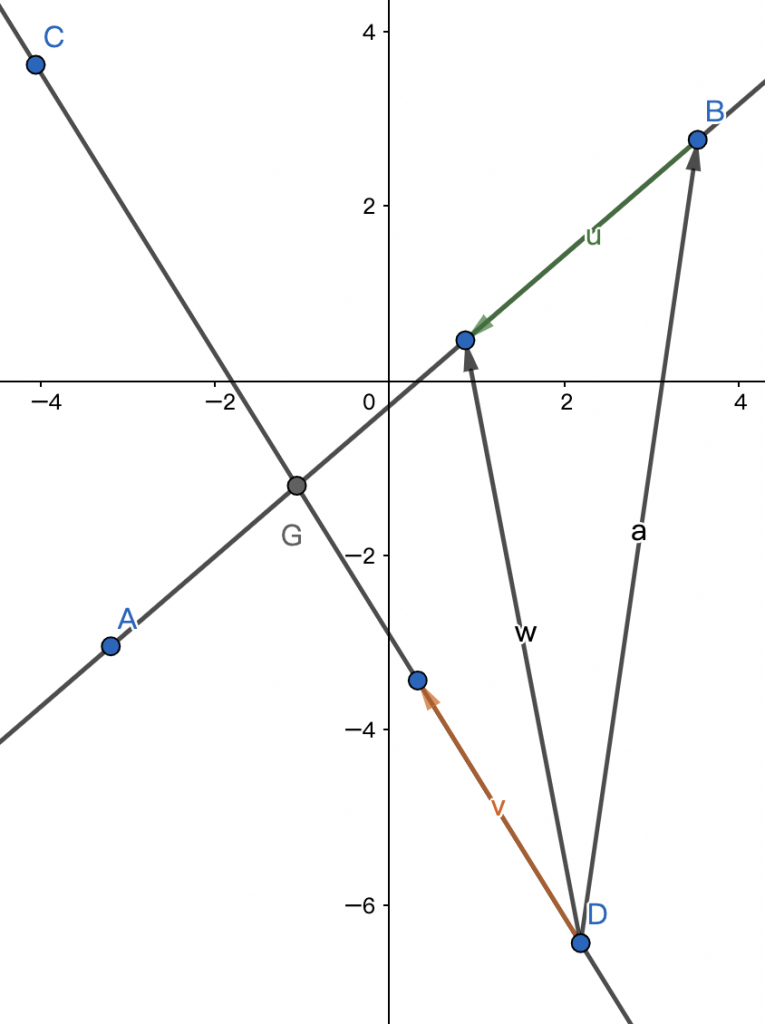
画个图:
如果我们要求点 G,由于我们知道点 \(B\) 的坐标,所以我们可以尝试把 \(\vec{BG}\) 求出来,然后加一下即可。求 \(\vec{BG}\) 并不难,可以考虑直接 \(\vec{BG} = \vec{u} \times \frac{|\vec{BG}|}{|\vec{u}|}\) 的思路去求。发现后面有一个比例一样的东西,这个东西我们可以考虑用向量叉积来表示,因为同底时面积比的含义就是高的比例。
vec intersect(vec a, vec b, vec c, vec d)
{
vec v = b - a, w = d - c, u = a - c;
return a + v * double((w ^ u) / (v ^ w));
}
求两个线段的交点
先做一遍相交性判断,然后在用两直线交点的做法搞即可。
点线距离
如果是线段的话,先要判段两个端点的长度。做这个点线距离其实就求平行四边形面积然后除掉底边即可。
多边形
凸包问题
先按 \(x\) 轴排序,然后维护一个叉积单调的单调栈即可。
// P2742.cpp
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#define pr pair<double, double>
using namespace std;
int n;
vector<pr> points;
deque<int> prs;
double getDist(pr a, pr b)
{
return sqrt((a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (a.second - b.second));
}
bool judge(int a, int b, int idx)
{
return (points[a].second - points[b].second) * (points[b].first - points[idx].first) >
(points[a].first - points[b].first) * (points[b].second - points[idx].second);
}
int main()
{
double ans = 0;
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
double x, y;
scanf("%lf%lf", &x, &y);
points.push_back(make_pair(x, y));
}
sort(points.begin(), points.end());
prs.push_front(0), prs.push_front(1);
for (int i = 2; i < n; i++)
{
while (prs.size() > 1 && !judge(prs[0], prs[1], i))
prs.pop_front();
prs.push_front(i);
}
for (int i = 0; i < prs.size() - 1; i++)
ans += getDist(points[prs[i]], points[prs[i + 1]]);
prs.clear();
prs.push_front(0), prs.push_front(1);
for (int i = 2; i < n; i++)
{
while (prs.size() > 1 && judge(prs[0], prs[1], i))
prs.pop_front();
prs.push_front(i);
}
for (int i = 0; i < prs.size() - 1; i++)
ans += getDist(points[prs[i]], points[prs[i + 1]]);
printf("%.2lf", ans);
return 0;
}
判断点与凸多边形的包含关系
凸多边形的面积
这个比较简单,直接:
\[ S = \frac{1}{2} \sum_{i = 1}^{n – 1} P_i \times P_{i + 1} i\]
记住这个“一般都不难”(划掉)
太难了(自闭