简述
在信息学竞赛中,多项式乘法出现得非常的多,朴素算法的时间复杂度为\(O(n^2)\),成为了许多毒瘤出题人卡指数的地方。所以,用快速傅立叶变换(FFT, Fast Fourier Transform)来优化多项式乘法是很有必要的。接下来,我会由浅入深地来介绍这两者与其之间的关系。
多项式
多项式一般定义为\(A(x) = \sum_{i = 0}^{n – 1} a_i x^i\),其中\(x\)为变量。多项式最高的次数为该多项式的度(degree)。一般,多项式有两种表达方式:
- 系数表达
- 点值表达
系数表达
\(A(x) = a_0 + a_1 x^1 + a_2 x^2 + \dots a_{n-1} x^{n-1}\)可以抽象为一个向量\((a_0, a_1, a_2, a_3, \dots a_{n-1})\)。每一个向量都可以与一个多项式一一对应,且,一般常用系数表达进行运算,所以基本上多项式乘法我们要求其用系数表达的向量作为输入和输出。
点值表达
对于一个多项式,给定\(n\)个数值\(x_0, x_1, x_2, \dots, x_{n-1}\)带入\(A(x)\)得到\(y_0, y_1, y_2, \dots, y_{n-1}\)即可确定一个度数为\(n-1\)的多项式。由点值表达转换到系数表达的方式叫做插值。
多项式乘法
多项式乘法在两种表达法下有不同的方式:
-
系数表达:
\[A(x) \times B(x) = \sum_{k = 0}^{2n-2} x^k \sum_{x = 0}^k a_i b_{k – i} \]
这样实现的时间复杂度是\(O(n^2)\),显然是很高的。 - 点值表达:\[ A(x_i) \times B(x_i) = A(x_i)B(x_i) \]复杂度为\(O(n)\)。
快速傅立叶变换 (Fast Fourier Transform)
快速傅立叶变换在信息学中可以用来加速卷积运算,在这篇文章里,我将介绍卷积运算的其中之一,也就是多项式的乘法。
如果要用快速傅立叶变换来优化多项式乘法,我们就需要首先理解大概的流程。使用 FFT 来加速多项式乘法一般的流程是:
- 将系数表达转换为点值表达,这一个部分我们用 FFT 进行优化。
- 然后\(O(n)\)求出点值表达下的多项式乘法。
- 用 IFT,也就是快速傅立叶逆变换,来把点值表达恢复成系数表达。
其中 FFT 和 IFT 的代码几乎一样,复杂度都为\(O(n \log n)\),整体复杂度为\(O(n \log n)\)。
现在开始正式讲解快速傅立叶变换的预备知识。
预备知识
复数中的虚数
复数域是目前最大的数域。一个复数可以分为两个部分:实部和虚部,写作:
\[ n = a + bi, i = \sqrt{-1} \]
其中,\(a\)是实部,\(bi\)是虚部。任意一个复数都可以在复平面上被表达:
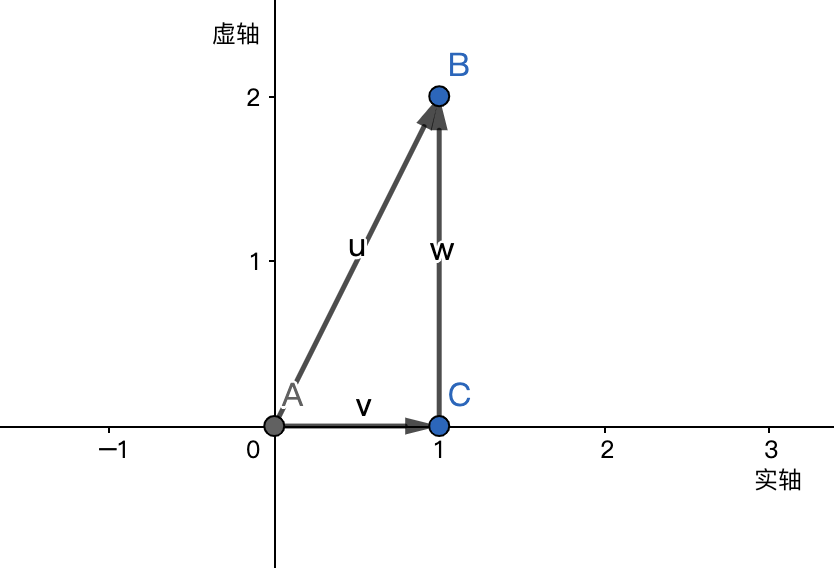
单位根
在复平面上,我们可以跟学习三角函数一样,作一个半径为\(1\)的单位元。其中,将这个圆\(n\)等分之后,这些点所代表的复数称之为单位根。其中,单位根可以被写作
\[\omega_n^k, k \in [0, n) \]
根据欧拉公式,有:
\[ e^{i\theta} = \sin \theta + i \cos \theta \]
单位根的性质
单位根的很多性质都像三角函数里面一样。这里介绍几种:
- 性质 1 \[ \omega_n^{kn} = \omega_n^0 \]
- 性质 2 \[ \omega_n^k = \omega_{\frac{n}{2}}^{\frac{k}{2}} \]
- 性质 3 \[ \omega_n^{k + \frac{n}{2}} = -\omega_n^k \]
单位根的指数是满足正常的运算法则的,体现在其可以写作\(e\)的幂的形式。
快速傅立叶变换的原理推导
我们现在知道\(A(x)\)的系数表达,现在我们要将其转换成点值表达。正常来讲,这个带入过程是\(O(n^2)\)的。但是,通过复数的性质,我们可以很快发现一些玄机。
为了方便,我们现在规定\(n = 2^x\)。考虑把\(A(x)\)分为奇偶两组:
\[ \begin{cases} A_1(x) = a_0 + a_2 x + a_4 x^2 + \dots + a_{n – 2}^{\frac{n}{2} – 1} \\ A_2(x) = a_1 + a_3 x + a_5 x^2 + \dots + a_{n – 1}^{\frac{n}{2} – 1} \end{cases} \\ A(x) = A_1(x^2) + x A_2(x^2) \]
我们现在要计算\( \sum_{k = 0}^{n – 1} A(\omega_n^{k}) \)。我们考虑把这个和式分开,变成两个部分:
\[ \sum_{k = 0}^{\frac{n}{2} – 1} A(\omega_n^k) + \sum_{k = 0}^{\frac{n}{2} – 1} A(\omega_n^{k + \frac{n}{2}}) \]
先来计算第一个部分:
\[ \begin{aligned} A(\omega_n^k) &= A_1(\omega_n^{2k}) + \omega_n^k A_2(\omega_n^{2k}) \\ &= A_1(\omega_{\frac{n}{2}}^k) + \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \end{aligned} \]
第二个部分:
\[ \begin{aligned} A(\omega_n^{k + \frac{n}{2}}) &= A_1(\omega_n^{2k + n}) + \omega_n^{k + \frac{n}{2}} A_2(\omega_n^{2k + n}) \\ &= A_1(\omega_n^{2k} \times \omega_n^n) – \omega_n^k A_2(\omega_n^{2k} \times \omega_n^n) \\ &= A_1(\omega_{\frac{n}{2}}^k) – \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \end{aligned} \]
对比推导结果:
\[ \begin{cases} \begin{aligned} A(\omega_n^k) &= A_1(\omega_{\frac{n}{2}}^k) + \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \\ A(\omega_n^{k + \frac{n}{2}}) &= A_1(\omega_{\frac{n}{2}}^k) – \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \end{aligned} \end{cases} \]
带入原来的和式:
\[ \sum_{k = 0}^{\frac{n}{2} – 1} A_1(\omega_{\frac{n}{2}}^k) + \omega_n^k A_2(\omega_{\frac{n}{2}}^k) , \sum_{k = 0}^{\frac{n}{2} – 1} A_1(\omega_{\frac{n}{2}}^k) – \omega_n^k A_2(\omega_{\frac{n}{2}}^k) \]
可以发现,整个计算过程最后只依赖于\([0, \frac{n}{2})\)区间,问题规模被缩小了一半。时间复杂度最后会变成\(O(n \log n)\),这个算法又叫做 Cooley-Tukey 算法。
快速傅立叶逆变换的原理推导
我们现在已经完成了快速傅立叶变换,假如我们已经搞定了点值乘法,那么现在我们要做的,就是把点值表达转换回系数表达。
我们现在已经把点值算完了,所以现在我们拿到的多项式是点值表示法\((y_0, y_1, y_2, \dots)\),现在考虑搞一个新的多项式\(B(x) = \sum_{i = 0}^{n – 1} y_i x^i\)。我们现在把一组与上面共轭的复数带入,得到\(B(x)\)的点值表示:
\[ \begin{aligned} c_k &= B(\omega_n^{-k}) = \sum_{i = 0}^{n – 1} y_i (\omega_n^{-k})^i \\ &= \sum_{i = 0}^{n – 1} (\sum_{j = 0}^{n – 1} a_j (\omega_n^i)^j )(\omega_n^{-ki}) \\ &= \sum_{i = 0}^{n – 1} \sum_{j = 0}^{n – 1} a_j \omega_n^{i(j – k)} \\ &= \sum_{i = 0}^{n – 1} \sum_{j = 0}^{n – 1} a_j (\omega_n^{j-k})^i \\ &= \sum_{j = 1}^{n – 1} a_j \sum_{i = 0}^{n – 1} (\omega_n^{j – k})^i \end{aligned} \]
发现后面的\(\sum_{i = 0}^{n – 1} (\omega_n^{j – k})^i\)是高中数学中的等比数列求和(这里感谢汪老师的教导),考虑写作:
\[ S(\omega_n^k) = 1 + \omega_n^k + \omega_n^{2k} + \dots + \omega_n^{(n – 1)k} \]
在\(n = k\)的情况下,显然\(S(\omega_n^k) = n\)。考虑\(n \neq k\)的情况:
\[ S(\omega_n^k) = \frac{1 – \omega_n^{nk}}{1 – \omega_n^k} = 0 \]
带入即可:
\[ \begin{aligned} c_k &= \sum_{j = 1}^{n – 1} a_j \sum_{i = 0}^{n – 1} (\omega_n^{j – k})^i \\ &= \sum_{j = 1}^{n – 1} a_j S(\omega_n^{j – k}) = na_k \end{aligned} \]
发现\(a_k = \frac{c_k}{n}\)。所以,逆变换时要与变换区分的地方有:
- 要让共轭复数参与运算。
- 算完了之后注意要除\(n\)。
实现
二进制位翻转
考虑枚举到边界的时候:
000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 7 0 2 4 6 - 1 3 5 7 0 4 - 2 6 - 1 5 - 3 7 0 - 4 - 2 - 6 - 1 - 5 - 3 - 7 000 100 010 110 001 101 011 111 // src: https://oi.men.ci/fft-notes/
蝴蝶操作就是多开个变量暂存,没了。
代码
// LOJ108.cpp
#include <bits/stdc++.h>
using namespace std;
typedef complex<double> cd;
const double Pi = acos(-1.0);
const int MAX_N = 3e5 + 2000;
cd A[MAX_N], B[MAX_N];
int n, m, rev[MAX_N], max_bit, max_power;
void fft_initialize()
{
for (max_bit = 1, max_power = 2; (1 << max_bit) < n + m - 1; max_bit++)
max_power <<= 1;
for (int i = 0; i < max_power; i++)
rev[i] = ((rev[i >> 1] >> 1) | ((i & 1) << (max_bit - 1)));
}
void fft(cd *arr, int len, int dft)
{
for (int i = 0; i < len; i++)
if (i < rev[i])
swap(arr[i], arr[rev[i]]);
for (int step = 1; step < len; step <<= 1)
{
cd omega_n = exp(cd(0, dft * Pi / step));
for (int j = 0; j < len; j += (step << 1))
{
cd omega_nk(1, 0);
for (int k = j; k < j + step; k++, omega_nk *= omega_n)
{
cd t = omega_nk * arr[k + step];
arr[k + step] = arr[k] - t;
arr[k] += t;
}
}
}
if (dft == -1)
for (int i = 0; i < len; i++)
arr[i] /= len;
}
int main()
{
scanf("%d%d", &n, &m), n++, m++, fft_initialize();
for (int i = 0, tmp; i < n; i++)
scanf("%d", &tmp), A[i].real(tmp);
for (int i = 0, tmp; i < m; i++)
scanf("%d", &tmp), B[i].real(tmp);
fft(A, max_power, 1), fft(B, max_power, 1);
for (int i = 0; i < max_power; i++)
A[i] *= B[i];
fft(A, max_power, -1);
for (int i = 0; i < n + m - 1; i++)
printf("%d ", (int)(A[i].real() + 0.5));
return 0;
}
