A – 非回文数字
这道题还没写,是一道数位 DP,推荐记忆化搜索。
B – 管道
这道题是一道相当好的题目。
首先对于\(m = n – 1\)的情况,也就是树的形态下,可以考虑自下向上推,也就是从叶子节点开始推起,参考代码中 Toposort 的写法。然后,对于\(m > n\)的情况可以直接输出\(0\),因为这个方程组并不存在唯一的解:\(m\)个未知数仅提供\(n\)个条件,这样是不成立的。
最后考虑\(m = n\)的情况。这种情况就是基环树了。首先,Toposort 会把支链上的答案全部统计完毕,并且合并到环上的点。最后,我们唯一要多做的事情,就是处理环上的方程组。考虑一个这样的环:
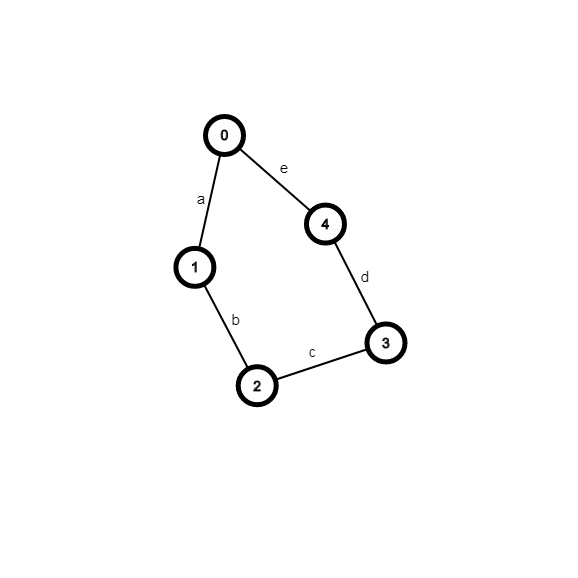
在环上点个数\(loopNum\)为奇数的情况下,有这样 5 个方程组成的方程组:
\[ \begin{cases} val(0) = e + a \\ val(1) = a + b \\ val(2) = b + c \\ val(3) = c + d \\ val(4) = d + e \end{cases} \]
通过一定顺序的相加和相减,我们至少可以解出一个未知数:
\[ val(0) – val(1) + val(2) – val(3) + val(4) = 2e \]
然而,在\(loopNum\)为偶数的情况下,这样的方程的结果就是\(0\),所以没法解。根据这样的方法,可以写出下面的代码:
// B.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 100100, MAX_E = 1000500;
int head[MAX_N], current, n, m, dat[MAX_N], anses[MAX_E], deg[MAX_N], loopNum;
bool tag[MAX_N];
struct edge
{
int id, to, nxt, weight;
} edges[MAX_E];
void addpath(int src, int dst, int id)
{
edges[current].to = dst, edges[current].nxt = head[src];
edges[current].id = id, head[src] = current++;
}
void toposort()
{
loopNum = n;
queue<int> q;
for (int i = 1; i <= n; i++)
if (deg[i] == 1)
q.push(i), loopNum--;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (deg[edges[i].to] != 0)
{
deg[u]--;
if ((--deg[edges[i].to]) == 1)
q.push(edges[i].to), loopNum--;
anses[edges[i].id] = 2 * (dat[u]);
dat[edges[i].to] -= dat[u], dat[u] = 0;
}
}
}
void preprocess(int u, int fa)
{
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (deg[edges[i].to] && edges[i].to != fa && tag[i] == false)
{
tag[i] = true, preprocess(edges[i].to, u);
return;
}
}
void dfs(int u, int fa, int lastEdge, int dep)
{
if (lastEdge != -1)
anses[edges[lastEdge].id] += (dep & 1) ? dat[u] : -dat[u];
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (tag[i])
{
if (lastEdge == i)
return;
dfs(edges[i].to, u, ((lastEdge == -1) ? i : lastEdge), dep + 1);
return;
}
}
void calc(int u, int fa, int lastEdge, int dep)
{
if (dep == loopNum)
return;
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (tag[i])
{
if (fa)
anses[edges[i].id] = -(anses[edges[lastEdge].id] - dat[u]) + dat[u];
calc(edges[i].to, u, i, dep + 1);
return;
}
}
int main()
{
memset(head, -1, sizeof(head));
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &dat[i]);
for (int i = 1, u, v; i <= m; i++)
scanf("%d%d", &u, &v), addpath(u, v, i), addpath(v, u, i), deg[u]++, deg[v]++;
if (m > n)
{
puts("0");
return 0;
}
toposort();
if (m == n)
{
if (loopNum % 2 == 0)
{
puts("0");
return 0;
}
for (int i = 1; i <= n; i++)
if (deg[i] > 0)
{
preprocess(i, 0);
dfs(i, 0, -1, 0);
calc(i, 0, 0, 0);
break;
}
}
for (int i = 1; i <= m; i++)
printf("%d\n", anses[i]);
return 0;
}
C – 牛棚安排
这道题太暴力了吧。
先说做法:用枚举+二分确定喜爱值区间,然后根据区间进行建图跑最大流。然而在这里,Dinic 和 ISAP 都会被卡…我又尝试了人人爱的#pragma GCC optimize (2)然而还是没啥用。所以,最后一个 TLE 的点,我就直接打表了(有更优做法记得评论)
// C.cpp
#pragma GCC optimize (2)
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 2020, MAX_M = 620400, INF = 0x3f3f3f3f;
int head[MAX_N], current, stat[MAX_N][22], srcPoint, destPoint, n, barnNum;
int dep[MAX_N], vis[MAX_N], cur[MAX_N], capacity[22], gap[MAX_N];
struct edge
{
int to, nxt, weight;
} edges[MAX_M];
void addpath(int src, int dst, int weight)
{
edges[current].to = dst, edges[current].nxt = head[src];
edges[current].weight = weight, head[src] = current++;
}
void addtube(int src, int dst, int weight)
{
addpath(src, dst, weight);
addpath(dst, src, 0);
}
void bfs()
{
memset(dep, 0, sizeof(dep)), memset(gap, 0, sizeof(gap));
queue<int> q;
q.push(destPoint), dep[destPoint] = 1, gap[1]++;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edges[i].nxt)
{
if (dep[edges[i].to] != 0)
continue;
q.push(edges[i].to), dep[edges[i].to] = dep[u] + 1;
gap[dep[edges[i].to]]++;
}
}
}
int dfs(int u, int flow, int &ans)
{
if (u == destPoint)
{
(ans += flow);
return flow;
}
int used = 0;
for (int i = head[u]; i != -1; i = edges[i].nxt)
if (edges[i].weight > 0 && dep[edges[i].to] + 1 == dep[u])
{
if (int di = dfs(edges[i].to, min(edges[i].weight, flow), ans))
edges[i].weight -= di, edges[i ^ 1].weight += di, used += di;
if (used == flow)
return used;
}
gap[dep[u]]--;
if (gap[dep[u]] == 0)
dep[srcPoint] = n + 1;
dep[u]++, gap[dep[u]]++;
return used;
}
int ISAP()
{
int ans = 0;
bfs();
while (dep[srcPoint] < n)
dfs(srcPoint, INF, ans);
return ans;
}
void build(int l, int r)
{
memset(head, -1, sizeof(head));
current = 0;
for (int i = 1; i <= n; i++)
for(int j = l; j <= r; j++)
addtube(i, stat[i][j] + n, 1);
for (int i = 1; i <= n; i++)
addtube(srcPoint, i, 1);
for (int i = 1; i <= barnNum; i++)
addtube(i + n, destPoint, capacity[i]);
}
bool check(int l, int r)
{
build(l, r);
return ISAP() == n;
}
int main()
{
scanf("%d%d", &n, &barnNum);
srcPoint = n + barnNum + 1, destPoint = srcPoint + 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= barnNum; j++)
scanf("%d", &stat[i][j]);
for (int i = 1; i <= barnNum; i++)
scanf("%d", &capacity[i]);
int minimumVal = INF, l = 1, r = barnNum;
if (n == 1000 && barnNum == 20)
{
bool flag = true;
for (int i = 1; i <= barnNum; i++)
if (stat[1][i] != i)
{
flag = false;
break;
}
if (flag)
{
puts("20");
return 0;
}
}
while(l <= r)
{
int gap = (l + r) >> 1;
bool flag = false;
for (int st = 1; st + gap - 1 <= n; st++)
{
int dst = st + gap - 1;
if (check(st, dst))
{
minimumVal = min(minimumVal, gap), r = gap - 1;
flag = true;
break;
}
}
if (!flag)
l = gap + 1;
}
printf("%d", minimumVal);
return 0;
}