简述
线性基应该算是线性代数范畴内的东西。在 OI 中,线性基被用来解决位运算或者是向量表示的问题。
建议读者学习了高中数学中的向量之后再来阅读本文,相信这样会帮助理解线性基。
线性空间
线性空间其实就是向量空间。一个线性空间其实就是无数个向量填充后的集合。通常来讲,一个线性空间可以由数乘向量和向量和的形式组成,也就是以下这种形式:
\[ k_1 \vec a_i + k_2 \vec a_j \]
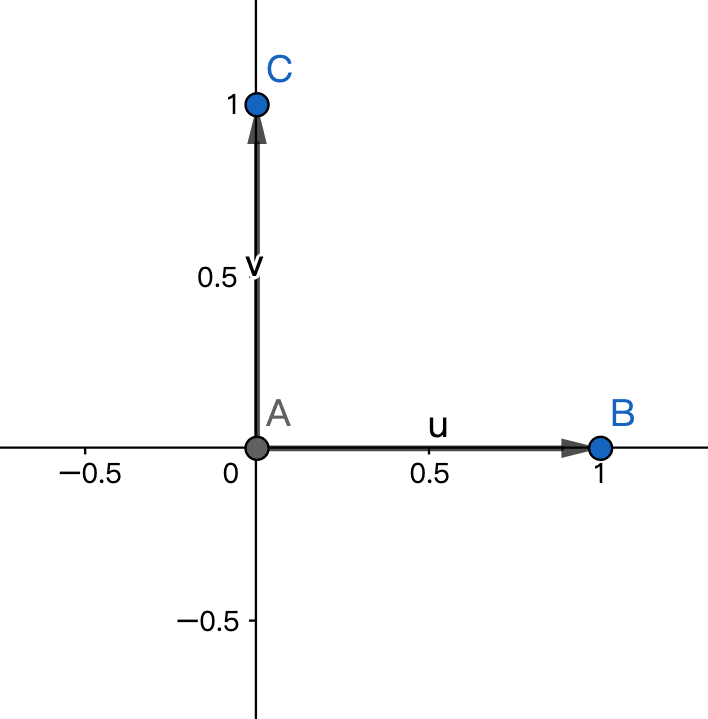
举个例子,二维平面的向量空间在坐标系上表示,就是无数种二维向量通过上面形式的运算所生成的向量集合。我们可以把这个理解为高中数学中的基底形式。我们知道,在二维向量空间内,\( (1, 0), (0, 1) \)这两种向量通过上面形式的运算就可以组成一个线性空间。我们称这个能生成整个二维线性空间的向量集合\( (1, 0), (0, 1) \)称为二维线性空间的生成子集。
更加规范的来讲,如果一个集合内的向量能通过向量积和的形式组成线性空间,则称这个集合为这个线性空间的生成子集。
我们现在来引入一些关于生成子集的内容。给定一个生成子集,如果存在一个\(\vec a_i = \sum_{\vec a_j \in S} k_j \vec a_j \),则称这些向量是线性相关的。换句话说,如果一个生成子集内存在一个向量能被子集内若干个除它本身的向量表示,那么称这些向量是线性相关的。如果一个生成子集内不存在线性相关的一些向量,那么称这个生成子集是线性无关的。线性无关的生成子集又被叫做基底(高中数学内容),简称基。对于一个线性空间的任何基的向量个数都相等,向量个数又叫做维数。
用矩阵表示生成子集
假设我们有一个在二维线性空间内的生成子集:\(S = \{ (1, 0), (0, 1), (2, 3), (3, 4) \}\)。我们可以用向量的横置矩阵表示法来表示每一个向量:
\[ \begin{bmatrix} 1 & 0 \end{bmatrix} \\ \begin{bmatrix} 0 & 1 \end{bmatrix} \\ \begin{bmatrix} 2 & 3 \end{bmatrix} \\ \begin{bmatrix} 3 & 4 \end{bmatrix} \]
我们可以把这些向量合并成一个增广矩阵(最后一列全部为 0 ):
\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 3 & 0 \\ 3 & 4 & 0 \end{bmatrix} \]
我们发现如果用高斯消元的方法来处理这个增广矩阵的话,会得出这样的结果:
\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \]
是的,第三行和第四行的主元位置全部变成了\(0\)。
我们发现这些矩阵中至多只有两行的主元不为 \(0\),而其他的位置都为\(0\)。每一种可能的矩阵其实就对应一种该生成子集的线性基,线性基内的元素在矩阵中主元位置不为\(0\)。所以,我们如果要求一组向量的线性基以及维数,只需要高斯消元就行了,非零主元的个数便是维数,其实维数也被称为一个矩阵的秩。
模板例题:BZOJ4004 [JLOI2015]装备购买
脸哥最近在玩一款神奇的游戏,这个游戏里有 \(n\) 件装备,每件装备有 \(m\) 个属性,用向量\(z_i(a_j, \dots ,a_m)\)表示 \((1 <= i <= n; 1 <= j <= m)\),每个装备需要花费 \(c_i\),现在脸哥想买一些装备,但是脸哥很穷,所以总是盘算着怎样才能花尽量少的钱买尽量多的装备。对于脸哥来说,如果一件装备的属性能用购买的其他装备组合出(也就是说脸哥可以利用手上的这些装备组合出这件装备的效果),那么这件装备就没有买的必要了。严格的定义是,如果脸哥买了 \(z_{i_1}, \dots, z_{i_p} \)这 \(p\) 件装备,那么对于任意待决定的 \(z_h\),不存在 \(b_1, \dots, b_p\) 使得 \( b_1 z_{i_1} + \dots + b_p z_{i_p} = z_h\)(\(b\) 是实数),那么脸哥就会买 \(z_h\),否则 \(z_h\) 对脸哥就是无用的了,自然不必购买。举个例子, \(z_1 =(1, 2, 3), z_2 =(3, 4, 5), z_h = (2, 3, 4)\),\(b_1 = \frac{1}{2},b_2 = \frac{1}{2}\),就有\( b_1 z_1 + b_2 z_2 = z_h\),那么如果脸哥买了 \(z_1\) 和 \(z_2\) 就不会再买 \(z_h\) 了。脸哥想要在买下最多数量的装备的情况下花最少的钱,你能帮他算一下吗?
其实这就是线性基的裸题,我们可以当作模板题来写。我们先记入所有的向量信息组成一个增广矩阵,然后我们在高斯消元中,选择主元时尽量选择花费小的向量就行了。下面是代码:
// BZ4004.cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 510;
const double eps = 1e-8;
long double mat[MAX_N][MAX_N], cost[MAX_N];
int n, m;
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%Lf", &mat[i][j]);
for (int i = 1; i <= n; i++)
scanf("%Lf", &cost[i]);
int dim = 0, ans = 0;
for (int i = 1; i <= n; i++)
{
int now = 0;
for (int j = dim + 1; j <= n; j++)
if (fabs(mat[j][i]) > eps && (now == 0 || cost[j] < cost[now]))
now = j;
if (now == 0)
continue;
dim++, ans += cost[now];
for (int j = 1; j <= m; j++)
swap(mat[dim][j], mat[now][j]);
swap(cost[dim], cost[now]);
for (int j = 1; j <= n; j++)
if (j != dim && fabs(mat[j][i]) > eps)
{
long double rate = mat[j][i] / mat[dim][i];
for (int k = i; k <= m; k++)
mat[j][k] -= rate * mat[dim][k];
}
}
printf("%d %d", dim, ans);
return 0;
}
线性基在位运算中的作用
线性基在信息学竞赛中,通常更多是用来解决位运算问题的,比如说集合中异或和最大的子集等问题。我们来探究子集异或和最大问题的解决方案:
先设\(S = \{a_1, a_2, a_3, \dots, a_n\}\)。我们要找的一个\(A \subset S\)使得\(xor_{a_i \in A} a_i\)最大。考虑用线性基的模型进行转换:我们找到整个\(S\)的线性基\(B\),也就是找到一个生成子集,其元素之间的异或可以组成\(S\)中所有的元素。转化模型时,可以把每个数的每一位二进制位作为向量的每一个维度对应的值,比如说\(9 = (1001)_2\),如果最高位数就是四位的话,那么这个向量可以表示成:
\[ \begin{bmatrix} 1 & 0 & 0 & 1 \end{bmatrix} \]
然后参与整个高斯消元的过程。高斯消元消完了之后,我们得到一个线性基\(B\),因为线性基上每一个向量只有一个位置上不为\(0\),所以我们在考虑最大异或和时,直接从高位开始遍历,遍历时检测线性基内是否存在某个向量在该维的值不为\(0\):如果有的话,就直接给答案加上贡献;如果没有,那么继续遍历。这样可以保证是最优的,因为高位的贡献比所有低位贡献都要大,所以优先考虑可以保证不会出现更大的答案,所以是最优的。
下面是代码(不用高斯消元,考虑新的方式搞定求线性基,请读者思考下面的方法):
// P3812.cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAX_N = 55;
ll arr[MAX_N], n, bit[70], ans;
int main()
{
scanf("%lld", &n);
for (int i = 1; i <= n; i++)
{
scanf("%lld", &arr[i]);
for (int pt = 62; pt >= 0; pt--)
{
if (((arr[i] >> (ll)pt) & 1) == 0)
continue;
if (bit[pt] == 0)
{
bit[pt] = arr[i];
break;
}
arr[i] ^= bit[pt];
}
}
for (int i = 62; i >= 0; i--)
if ((ans ^ bit[i]) > ans)
ans ^= bit[i];
printf("%lld", ans);
return 0;
}
位运算线性基的一些性质
- 线性基中数的个数一定是最小的
- 线性基中的数无法表示出 0。