简述
主席树是一个很有意思的数据结构,其全称其实是「可持久化线段树」,至于为什么叫「主席树」是因为:
由于发明者黄嘉泰姓名的缩写与前中共中央总书记、国家主席胡锦涛(H.J.T.)相同,因此这种数据结构也可被称为总书记树或主席树。
From Wikipedia.org
主席树的结构
主席树是一种可持久化的数据结构。何为「可持久化」?「可持久化」的意思是我们可以访问历史版本,每一次线段树被操作就会产生一个新的历史版本,与旧版本分开。暴力思路是我们可以每一次更改时都存一份,但是这样铁定会\(MLE\),所以我们需要利用已有信息来进行空间压缩。我们先思考一颗支持单点修改、区间查询的线段树的可持久化方法:
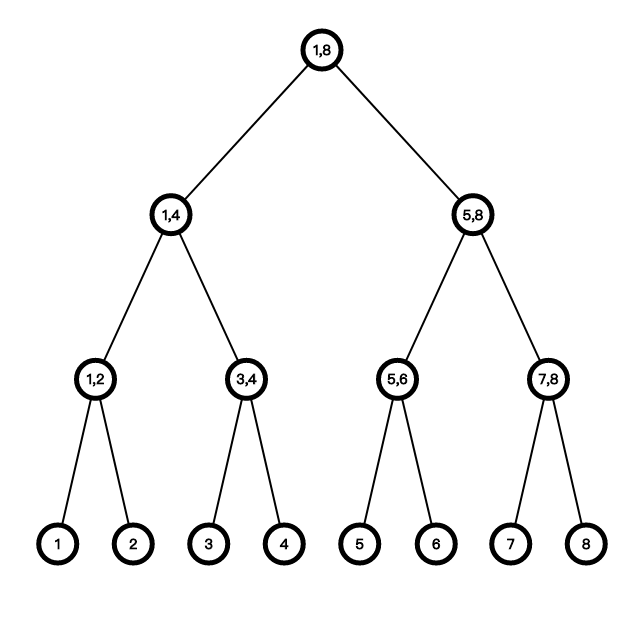
如果我们这个时候操作下标为 3 的节点,我们如何保存旧版本和新产生的版本呢?首先我们注意到,操作一个单点时,线段树中最多有\(log \ n\)个点会被修改。我们可以只考虑这\(log \ n\)个点。注意,这里需要动态开点,因为我们要在当前系统下新建一颗树,左右儿子的规律不再适用。我们现在修改 3,把经过的点全部复制一份,然后把空的左右儿子连接到之前的地方:
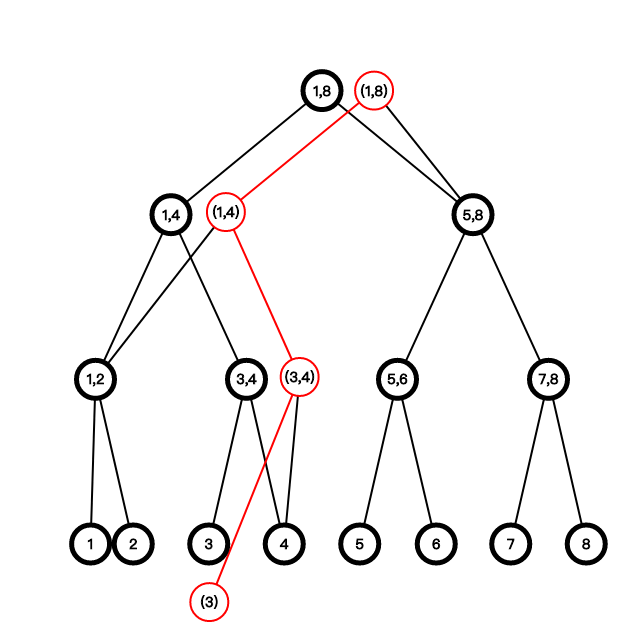
这样我们只添加了\(log \ n\)个节点。这样非常省空间,假设有\(s\)次操作,那么空间只需要\(n \log n + s \log n\)就 OK 了。
// Example on sustainable segment tree;
const int MAX_N = 1e5 + 2000;
struct node
{
int sum, lson, rson;
} nodes[MAX_N << 4];
// the entries for the history versions;
int roots[MAX_N];
// the amount of the nodes in the system;
int tot;
// generate the tree and return the new created node id.
int build(int l, int r)
{
int p = ++tot;
if (l == r)
return p;
int mid = (l + r) >> 1;
nodes[p].lson = build(l, mid), nodes[p].rson = build(mid + 1, r);
return p;
}
// given the previous version, to generate a new version since the update;
int update(int qx, int l, int r, int pre, int val)
{
int p = ++tot;
// copy the info and update;
nodes[p] = nodes[pre], nodes[p].sum += val;
if (l == r)
return p;
int mid = (l + r) >> 1;
// to edit son nodes;
if (qx <= mid)
nodes[p].lson = update(qx, l, mid, nodes[pre].lson, val);
else
nodes[p].rson = update(qx, mid + 1, r, nodes[pre].rson, val);
return p;
}
适用场景 A:第 k 小问题
例题:POJ2104
解决这个问题之前,建议先学习权值线段树的概念(下标为数,维护区间内数字出现的次数)。
区间内的第\(k\)小问题其实也可以像在权值线段树内解决一样轻松。我们可以维护数字出现次数的前缀和,然后就可以像在权值线段树内一样,顺着次数的大小关系找出第\(k\)大,询问代码如下:
int query(int l, int r, int previous, int now, int k)
{
int lsWeight = sum[nodes[now].lson] - sum[nodes[previous].lson];
if (l == r)
return l;
if (k <= lsWeight)
return query(l, mid, nodes[previous].lson, nodes[now].lson, k);
else
return query(mid + 1, r, nodes[previous].rson, nodes[now].rson, k - lsWeight);
}
适用场景 B:排列的区间交集
其实去掉排列这个限制也能做(进行离散化即可)。为了方便表述,我们设定一个说法:排列 \(A[1-n], B[1-m]\)。
我们可以先把\(A\)中数字的出现位置都记录下来,也就是\(pos[A[i]]=i\)。然后考虑把\(B\)放进主席树来进行维护。还是权值线段树的思想,我们每一次将\(B\)中的数字按顺序、以\(pos[B[i]]\)为坐标放入主席树,我们也就可以在回答\(A[l_1 – r_1] \cap B[l_2 – r_2]\)时,用 \(r_2\)的版本查询\([l_1 – r_1]\)的数字出现次数前缀和 减去 \(l_2 – 1\)的版本查询\([l_1 – r_1]\)的数字出现次数前缀和 就可以知道这两段区间共有的交集元素个数了。
代码写出来是这样的:
int query(int ql, int qr, int l, int r, int p)
{
if (ql <= l && r <= qr)
return nodes[p].sum;
int mid = (l + r) >> 1, ans = 0;
if (ql <= mid)
ans = query(ql, qr, l, mid, nodes[p].lson);
if (mid < qr)
ans += query(ql, qr, mid + 1, r, nodes[p].rson);
return ans;
}
int inquire(int l1, int r1, int l2, int r2)
{
return query(l1, r1, 1, n, roots[r2]) - query(l1, r1, 1, n, roots[l1 - 1]);
}
void build(int a[], int b[], int n, int m)
{
int pos[n];
for (int i = 1; i <= n; i++)
pos[a[i]] = i;
for (int i = 1; i <= m; i++)
roots[i] = update(pos[b[i]], 1, n, roots[i - 1], 1);
}
先写这么多,待会再补。

催更!(